Abstract:
We simulate interaction quenches crossing from a superfluid to a supersolid state in a dipolar quantum gas of 164Dy atoms, trapped in an elongated tube with periodic boundary conditions, via the extended Gross-Pitaevskii equation. A freeze-out time is observed through a delay in supersolid formation after crossing the critical point. We compute the density-density correlations at the freeze-out time and extract the frozen correlation length for the solid order. An analysis of the freeze-out time and correlation length versus the interaction quench rate allows us to extract universal exponents corresponding to the relaxation time and correlation length based on predictions of the Kibble-Zurek mechanism. Over several orders of magnitude, clear power-law scaling is observed for both the freeze-out time and the correlation length, and the corresponding exponents are compatible with predictions based on the excitation spectrum calculated via Bogoliubov theory. Defects due to independent local breaking of translational symmetry, contributing to globally incommensurate supersolid order, are identified, and their number at the freeze-out time is found to also scale as a power law. Our results support the hypothesis of a continuous transition whose universality class remains to be determined but appears to differ from that of the (1 + 1)-dimensional XY model.
W. Kirkby, H. Salman, T. Gasenzer, L. Chomaz, „Kibble-Zurek scaling of the superfluid-supersolid
transition in an elongated dipolar gas“, Phys. Rev. Res. 7, 023248 (2025).
https://journals.aps.org/prresearch/abstract/10.1103/x51r-vdyf
Related to Project A07
Abstract:
Nonlinearities in King plots (KP) of isotope shifts (IS) can reveal the existence of beyond-standard-model (BSM) interactions that couple electrons and neutrons. However, it is crucial to distinguish higher-order standard model (SM) effects from BSM physics. We measure the IS of the transitions 3𝑃0→3𝑃1 in Ca14+ and 2𝑆1/2→2𝐷5/2 in Ca+ with sub-Hz precision as well as the nuclear mass ratios with relative uncertainties below 4 ×10−11 for the five stable, even isotopes of calcium (40,42,44,46,48Ca). Combined, these measurements yield a calcium KP nonlinearity with a significance of ∼103𝜎. Precision calculations show that the nonlinearity cannot be fully accounted for by the expected largest higher-order SM effect, the second-order mass shift, and identify the little-studied nuclear polarization as the only remaining SM contribution that may be large enough to explain it. Despite the observed nonlinearity, we improve existing KP-based constraints on a hypothetical Yukawa interaction for most of the new boson masses between 10 eV/c2 and 107 eV/c2.
M. Door, S. Eliseev, P. Filianin, J. Herkenhoff, K. Kromer, K. Blaum et al., „Nonlinear Calcium
King Plot Constrains New Bosons and Nuclear Properties“, Phys. Rev. Lett. 134, 233002
(2025).
https://journals.aps.org/prl/abstract/10.1103/PhysRevLett.134.233002
Related to Project B01, B02
Abstract:
While the abundances of the final state hadrons in relativistic heavy-ion collisions are rather well described by the thermal particle production, the shape of the transverse momentum, p_T , distribution below p_T ≈ 500 MeV/c, is still poorly understood. We propose a procedure to quantify the model-to-data differences using Bayesian inference techniques, which allows for consistent treatment of the experimental uncertainties and tests the completeness of the available hydrodynamic frameworks. Using relativistic fluid framework FluiduM with PCE coupled to TrENTo initial state and FastReso decays, we analyze p_T distribution of identified charged hadrons measured in heavy-ion collisions at top RHIC and the LHC energies and identify an excess of pions produced below p_T ≈ 500 MeV/c. Our results provide new input for the interpretation of the pion excess as either missing components in the thermal particle yield description or as an evidence for a different particle production mechanism.
P. Lu, R. Kavak, A. Dubla, S. Masciocchi, I. Selyuzhenkov, „Quantification of the low- pT pion
excess in heavy-ion collisions at the LHC and top RHIC energy“, Nucl.Sci.Tech. 36, 142 (2025).
https://link.springer.com/article/10.1007/s41365-025-01718-z
Related to Project C06
Abstract:
Driven systems are of fundamental scientific interest, as they can exhibit properties distinct from the same system at equilibrium. In certain cases, long-lived states of driven matter can emerge with new material properties. Here we probe the excitation spectrum of an emergent patterned state in a driven superfluid and find that its response is identical to that of a one-dimensional supersolid. By preparing wave packets as well as specific collective modes and probing their dynamics, we identify two distinct sound modes associated with spontaneously broken U(1) and translational symmetries. Consistent with the hydrodynamic description of superfluid smectics, longitudinal excitations propagate with finite velocities, whereas transverse perturbations exhibit diffusive behaviour. These results demonstrate how the conceptual framework of supersolidity can be used to characterize dynamic and far-from-equilibrium states.
N. Liebster, M. Sparn, E. Kath, J. Duchene, H. Strobel, M. K. Oberthaler, „Supersolid-like
sound modes in a driven quantum gas“, Nat. Phys. 2025 (2025).
https://www.nature.com/articles/s41567-025-02927-4
Related to Project B04
Abstract:
The emergence of distinctly sub-diffusive scaling in the vicinity of an anomalous non-thermal fixed point is discussed in a quasi-two-dimensional dipolar Bose gas in the superfluid phase, carrying ensembles of vortices and antivortices with zero net angular momentum. The observed scaling behavior reflects coarsening dynamics driven by the mutual annihilation of vortices and antivortices, with the mean inter-defect distance growing algebraically over time as 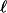

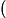
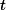

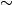
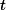
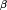 . A sub-diffusive (
. A sub-diffusive (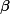

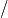
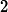 ) exponent
) exponent 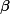
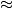
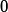

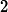 is extracted for various parameter regimes, initial conditions, and dipolar configurations from both scaling occupation-number spectra and the evolution of inter-defect distances as well as the corresponding total vortex densities. As vortex-antivortex annihilation progresses, excitations of the background condensate increase. This gives rise to a transition in the scaling behavior at late times, toward a non-thermal fixed point governed by diffusion-type scaling with
is extracted for various parameter regimes, initial conditions, and dipolar configurations from both scaling occupation-number spectra and the evolution of inter-defect distances as well as the corresponding total vortex densities. As vortex-antivortex annihilation progresses, excitations of the background condensate increase. This gives rise to a transition in the scaling behavior at late times, toward a non-thermal fixed point governed by diffusion-type scaling with 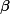
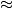
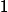
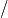
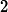 as expected for the mutual annihilation of well-separated vortex-antivortex dipoles. While the temporal scaling with
as expected for the mutual annihilation of well-separated vortex-antivortex dipoles. While the temporal scaling with 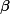 does not depend significantly on the strength and anisotropy of the dipolar interactions and thus underlines the universality of the anomalous as well as diffusion-type non-thermal fixed points, we find distinctly different vortex patterns resulting in the dipolar case. While in the superfluid with contact interactions only, same-sign vortices tend to cluster and form large-scale eddies, in the dipolar and tilted cases, roton excitations appear to prevent such motion, giving rather rise to a maximisation of distances between vortices of either sign.
does not depend significantly on the strength and anisotropy of the dipolar interactions and thus underlines the universality of the anomalous as well as diffusion-type non-thermal fixed points, we find distinctly different vortex patterns resulting in the dipolar case. While in the superfluid with contact interactions only, same-sign vortices tend to cluster and form large-scale eddies, in the dipolar and tilted cases, roton excitations appear to prevent such motion, giving rather rise to a maximisation of distances between vortices of either sign.
N. Rasch, L. Chomaz, T. Gasenzer, „Anomalous non-thermal fixed point in a quasi-twodimensional
dipolar Bose gas“, 2. Juni 2025, arXiv:2506.01653 (2025).
https://arxiv.org/abs/2506.01653
Related to Project A07
Abstract:
Magnetic moments of bound-electron systems are a sensitive tool for testing fundamental interactions. The g factors of lithium-like ions have been rigorously studied in recent years, enabling insights into the relativistic interelectronic effects. In this work, we present the g-factor measurement of lithium-like tin, accurate to 0.5 parts per billion, as well as ab initio theoretical calculations that include an advanced treatment of the interelectronic interaction. We further improved the prediction by using the experimental result for the hydrogen-like tin g factor, inferring from it the unknown higher-order quantum electrodynamic (QED) effects. The observed agreement independently confirms the revised theory at a previously inaccessible high atomic number Z of 50, where QED effects are considerably larger.
J. Morgner, V. A. Yerokhin, C. M. König, F. Heiße, B. Tu, T. Sailer, B. Sikora, Z. Harman,
J. R. C. López-Urrutia, C. H. Keitel, S. Sturm, K. Blaum, „Testing interelectronic interaction
in lithium-like tin“, Science 388, 945 (2025).
https://www.science.org/doi/10.1126/science.adn5981
Related to Project B01, B02
Abstract:
Dense quantum chromodynamics (QCD) matter may exhibit crystalline phases. Their existence is reflected in a moat regime, where mesonic correlations feature spatial modulations. We study the real-time properties of pions at finite temperature and density in QCD in order to elucidate the nature of this regime. We show that the moat regime arises from particle-hole-like fluctuations near the Fermi surface. This gives rise to a characteristic peak in the spectral function of the pion at nonzero spacelike momentum. This peak can be interpreted as a new quasi particle, the moaton. In addition, our framework also allows us to directly test the stability of the homogeneous chiral phase against the formation of an inhomogeneous condensate in QCD. We find that an inhomogeneous instability is highly unlikely for baryon chemical potentials 𝜇𝐵≤630 MeV.
W.-j. Fu, J. M. Pawlowski, R. D. Pisarski, F. Rennecke, R. Wen, S. Yin, „QCD moat regime
and its real-time properties“, Phys. Rev. D 111, 094026 (2025).
https://journals.aps.org/prd/abstract/10.1103/PhysRevD.111.094026
Related to Project B03
Abstract:
The chiral crossover of QCD at finite temperature and vanishing baryon density turns into a second-order phase transition if lighter than physical quark masses are considered. If this transition occurs sufficiently close to the physical point, its universal critical behavior would largely control the physics of the QCD phase transition. We quantify the size of this region in QCD using the functional renormalization group. This allows us to study both critical and noncritical effects on equal footing, facilitating a precise determination of the scaling regime. We find that the physical point is far away from the critical region. Importantly, we show that the physics of the chiral crossover is dominated by soft modes even far beyond the critical region. While scaling functions determine all thermodynamic properties of the system in the critical region, the order parameter potential is the relevant quantity away from it. We compute this potential in QCD using the functional renormalization group and Dyson-Schwinger equations and provide a simple parametrization for phenomenological applications.
J. Braun, Y.-R. Chen, W.-J. Fu, F. Gao, C. Huang, F. Ihssen, J. M. Pawlowski, F. Rennecke,
F. R. Sattler, Y.-Y. Tan, R. Wen, S. Yin, „Soft modes in hot QCD matter“, Phys. Rev. D 111,
094010 (2025).
https://journals.aps.org/prd/abstract/10.1103/PhysRevD.111.094010
Related to Project A02, B03, C01
Abstract:
Nonthermal fixed points are paradigmatic far-from-equilibrium phenomena of relevance to high-energy physics, cosmology, and cold atomic gases. We propose that, despite their intrinsically nonequilibrium nature, nonthermal fixed points give rise to hydrodynamic excitations otherwise known in the vicinity of thermal equilibrium. As a result, nonthermal fixed points can also be characterized by transport coefficients, such as a far-from-equilibrium, and therefore manifestly time-dependent, incarnation of shear viscosity. We corroborate our proposal with explicit studies using relativistic kinetic theory with binary collisions of massless particles in the 14-moment approximation and comparisons to QCD kinetic theory simulations.
J. Berges, G. S. Denicol, M. P. Heller, T. Preis, „Far from equilibrium hydrodynamics of nonthermal
fixed points“, 26. Apr. 2025, arXiv:2504.18754 (2025).
https://arxiv.org/abs/2504.18754
Related to Project B03
Abstract:
We compute from first principles the dispersion relation 
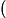
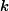
 of a dipolar Bose gas of erbium atoms close to the roton instability by employing the Complex Langevin (CL) algorithm. Other than the path integral Monte Carlo algorithm, which samples the quantum mechanical path integral in the
of a dipolar Bose gas of erbium atoms close to the roton instability by employing the Complex Langevin (CL) algorithm. Other than the path integral Monte Carlo algorithm, which samples the quantum mechanical path integral in the 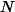 -particle basis, CL samples the field-theoretic path integral of interacting bosons and can be evaluated for experimentally realistic atom numbers. We extract the energy of roton excitations as a function of the s-wave scattering length, and compare our results to those from Gross-Pitaevskii theory, with and without quantum fluctuation corrections.
-particle basis, CL samples the field-theoretic path integral of interacting bosons and can be evaluated for experimentally realistic atom numbers. We extract the energy of roton excitations as a function of the s-wave scattering length, and compare our results to those from Gross-Pitaevskii theory, with and without quantum fluctuation corrections.
P. Heinen, W. Kirkby, L. Chomaz, T. Gasenzer, „Ab initio Complex Langevin computation
of the roton gap for a dipolar Bose condensate“, 25. Apr. 2025, arXiv:2504.18709 (2025).
https://arxiv.org/abs/2504.18709
Related to Project A07
Abstract:
Probabilistic cellular automata with deterministic updating are discrete quantum systems. They are characterized by a probability distribution over initial configurations. We employ the quantum formalism for an investigation of random probabilistic cellular automata for which the properties of the deterministic updating are randomly distributed over space and time. We are interested in a possible continuum limit for a very large number of cells or space points. We consider bits with two colors, moving to the left or right on a linear chain. At randomly distributed scattering points they change direction and color. A numerical simulation reveals the typical features of quantum systems. We find particular initial probability distributions which reemerge periodically after a certain number of time steps, as produced by the periodic evolution of energy eigenstates in quantum mechanics. Using a description in terms of wave functions allows us to introduce statistical observables for momentum and energy. They characterize the probabilistic information without taking definite values for a given bit configuration, with a conceptual status similar to temperature in classical statistical thermal equilibrium. Conservation of energy and momentum are essential ingredients for the understanding of the evolution of the stochastic probabilistic automata. This evolution resembles in some aspects a single Dirac fermion in two dimensions with a generalized random potential.
A. Kreuzkamp, C. Wetterich, „Quantum systems from random probabilistic automata“,
Phys. Rev. A 111, 042213 (2025).
https://journals.aps.org/pra/abstract/10.1103/PhysRevA.111.042213
Related to Project C01
Abstract:
The approximate SACOT-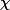 scheme for heavy quark production in deep-inelastic scattering was initially formulated for the neutral current structure functions
scheme for heavy quark production in deep-inelastic scattering was initially formulated for the neutral current structure functions 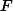
 and
and 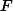
 . We extend this approach to the charged current case (also including
. We extend this approach to the charged current case (also including 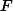
 ), and thereby complete the definitions for the most relevant inclusive structure functions. Furthermore, we implement these structure functions in the open-source code
), and thereby complete the definitions for the most relevant inclusive structure functions. Furthermore, we implement these structure functions in the open-source code 

 which provides fast numerical evaluations over a wide kinematic range; this addition to the
which provides fast numerical evaluations over a wide kinematic range; this addition to the 
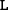

 code is publicly available, with details provided in the appendix. This SACOT-
code is publicly available, with details provided in the appendix. This SACOT-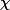 implementation enables, for the first time, detailed numerical insights on the mass dependence of the structure functions and cross sections in the
implementation enables, for the first time, detailed numerical insights on the mass dependence of the structure functions and cross sections in the 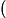


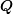

 -plane for both neutral and charged current processes. We consider kinematic regions relevant for the experimental measurements from fixed-target
-plane for both neutral and charged current processes. We consider kinematic regions relevant for the experimental measurements from fixed-target  DIS experiments (NuTeV, CCFR and Chorus) and HERA, and also projections for the upcoming EIC. In particular, the
DIS experiments (NuTeV, CCFR and Chorus) and HERA, and also projections for the upcoming EIC. In particular, the  DIS experiments reveal a surprisingly strong dependence on the mass effects, offering valuable insights that may help resolve long-standing challenges in accurately describing these datasets.
DIS experiments reveal a surprisingly strong dependence on the mass effects, offering valuable insights that may help resolve long-standing challenges in accurately describing these datasets.
P. Risse, V. Bertone, T. Jezo, K. Kovarík, A. Kusina, F. Olness, I. Schienbein, „Heavy Quark
mass effects in charged-current Deep-Inelastic Scattering at NNLO in the ACOT scheme“,
17. Apr. 2025, arXiv:2504.13317 (2025).
https://arxiv.org/abs/2504.13317
Related to Project C05
Abstract:
A decade ago, a universal stabilization mechanism driven by quantum fluctuations was discovered in ultracold Bose gases of highly magnetic atoms. This mechanism prevents these systems from collapsing and instead allows exotic states of matter to arise, including ultradilute quantum droplets, crystallized quantum states, and specifically supersolids. We review the experimental and theoretical progress in understanding these quantum-stabilized states, their emergence, and intriguing properties.
L. Chomaz, „Quantum-stabilized states in magnetic dipolar quantum gases“, 8. Apr. 2025,
arXiv:2504.06221 (2025).
https://arxiv.org/abs/2504.06221
Related to Project A07
Abstract:
We evaluate thermodynamic observables such as pressure, baryon number, entropy and energy density, as well as the second and fourth order baryon number cumulants in the phase structure of QCD. The intertwined confinement and chiral dynamics is resolved within functional QCD, aiming for quantitative accuracy at larger densities. Specifically it is shown that the self-consistent resolution of the confining gluonic background is crucial in particular for even the qualitative properties of the cumulants. Our results are in quantitative agreement with lattice and functional QCD benchmarks at vanishing and small chemical potentials. Moreover, they offer novel insights in the dynamics at larger chemical potentials including the regime of the critical end point. A welcome by-product of this analysis is the computation of the Polyakov loop potential in finite density QCD, which, alongside the aforementioned observables, can be used as input and benchmark for effective theory computations at finite density.
Y. Lu, F. Gao, Y.-x. Liu, J. M. Pawlowski, „Finite density signatures of confining and chiral
dynamics in QCD thermodynamics and fluctuations of conserved charges“, 7. Apr. 2025,
arXiv:2504.05099 (2025).
https://arxiv.org/abs/2504.05099
Related to Project B03
Abstract:
We solve the anharmonic oscillator with physics-informed renormalisation group (PIRG) flows, with an emphasis on the weak coupling regime with its instanton-dominated tunnelling processes. We show that the instanton physics behind the exponential decay of the energy gap is already covered in the first order of the derivative expansion of the PIRG. The crucial new ingredients in the present analysis are the use of the ground state expansion within PIRG flows, as well as precision numerics based on Galerkin methods. Our result 





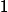

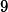
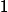
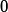
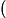
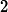
 for the decay constant is in quantitative agreement with the analytic one,
for the decay constant is in quantitative agreement with the analytic one, 





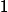

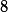
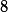
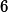 with a deviation of
with a deviation of 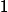
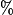 . This illustrates very impressively the capacity of the PIRG for fully capturing non-perturbative physics already in relatively simple approximations.
. This illustrates very impressively the capacity of the PIRG for fully capturing non-perturbative physics already in relatively simple approximations.
A. Bonanno, F. Ihssen, J. M. Pawlowski, „Tunneling with physics-informed RG flows in the
anharmonic oscillator“, 4. Apr. 2025, arXiv:2504.03437 (2025).
https://arxiv.org/abs/2504.03437
Related to Project A02
Abstract:
We discuss the universal non-equilibrium enhancement of long-wavelength Goldstone bosons induced by quenches to broken phase in Model G — the dynamical universality class of an 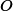
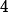
 -antiferromagnet and chiral QCD phase transition. Generic scaling arguments predict a parametric enhancement in the infrared spectra of Goldstones, which is confirmed by fully-fledged stochastic simulations. The details of the enhancement are determined by the non-linear dynamics of a superfluid effective theory, which is a limit of Model G reflecting the broken
-antiferromagnet and chiral QCD phase transition. Generic scaling arguments predict a parametric enhancement in the infrared spectra of Goldstones, which is confirmed by fully-fledged stochastic simulations. The details of the enhancement are determined by the non-linear dynamics of a superfluid effective theory, which is a limit of Model G reflecting the broken 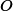
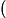
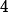
 symmetry. Our results translate to a parametric enhancement of low-momentum pions in heavy-ion collisions at the LHC, which are underpredicted in current hydrodynamic models without critical dynamics.
symmetry. Our results translate to a parametric enhancement of low-momentum pions in heavy-ion collisions at the LHC, which are underpredicted in current hydrodynamic models without critical dynamics.
A. Florio, E. Grossi, A. Mazeliauskas, A. Soloviev, D. Teaney, „Supercooled Goldstones at the
QCD chiral phase transition“, 4. Apr. 2025, arXiv:2504.03516 (2025).
https://arxiv.org/abs/2504.03516
Related to Project A01
Abstract:
We present a detailed numerical and analytical study of the out-of-equilibrium dynamics of Model G, the dynamical universality class relevant to the chiral phase transition. We perform numerical 3D stochastic (Langevin) simulations of the 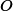
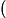
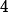
 critical point for large lattices in the chiral limit. We quench the system from the high-temperature unbroken phase to the broken phase and study the non-equilibrium dynamics of pion fields. Strikingly, the non-equilibrium evolution of the two-point functions exhibits a regime of growth, a parametrically large enhancement, and a subsequent slow relaxation to equilibrium. We analyze our numerical results using dynamic critical scaling and mean-field theory. The growth of the two point functions is determined by the non-linear dynamics of an ideal non-abelian superfluid, which is a limit of Model G that reflects the broken chiral symmetry. We also relate the non-equilibrium two-point functions to a long-lived parametric enhancement of soft pion yields relative to thermal equilibrium following a quench.
critical point for large lattices in the chiral limit. We quench the system from the high-temperature unbroken phase to the broken phase and study the non-equilibrium dynamics of pion fields. Strikingly, the non-equilibrium evolution of the two-point functions exhibits a regime of growth, a parametrically large enhancement, and a subsequent slow relaxation to equilibrium. We analyze our numerical results using dynamic critical scaling and mean-field theory. The growth of the two point functions is determined by the non-linear dynamics of an ideal non-abelian superfluid, which is a limit of Model G that reflects the broken chiral symmetry. We also relate the non-equilibrium two-point functions to a long-lived parametric enhancement of soft pion yields relative to thermal equilibrium following a quench.
A. Florio, E. Grossi, A. Mazeliauskas, A. Soloviev, D. Teaney, „Quenching through the QCD
chiral phase transition“, 4. Apr. 2025, arXiv:2504.03514 (2025).
https://arxiv.org/abs/2504.03514
Related to Project A01
Abstract:
In this work, we perform computations of inclusive jet, and semi-inclusive jet-hadron cross sections for minimum bias oxygen-oxygen collisions at RHIC and LHC collision energies. We compute the no-quenching baseline for the jet nuclear modification factor RAA and jet-, and hadron-triggered semi-inclusive nuclear modification factors IAA. We do this with state-of-the-art nuclear parton distribution functions (nPDFs), next-to-leading-order matrix elements, parton shower, and hadronization. We observe deviations from unity due to cold-nuclear matter effects, even without quenching. We demonstrate that the parton distribution uncertainties constitute a significant obstacle in detecting energy loss in small collision systems. Hadron-triggered observables are particularly sensitive to uncertainties due to correlations between the trigger and analyzed particles. For jet-triggered IAA, there exists a kinematic window in which nPDF and scale uncertainties cancel dramatically while showing little sensitivity to parton shower and hadronization models, addressing a major limiting factor for energy loss discovery in small systems.
J. Gebhard, A. Mazeliauskas, A. Takacs, „No-quenching baseline for energy loss signals in
oxygen-oxygen collisions“, JHEP 2025, 34 (2025).
https://link.springer.com/article/10.1007/JHEP04(2025)034
Related to Project A01
Abstract:
We investigate the information extractable from measurement distributions of two non-commuting spin observables in a multi-well spin-1 Bose–Einstein condensate. We provide a variety of analytic and numerical evidence that suitably chosen classical entropies and classical mutual informations thereof contain the typical feature of quantum entropies known in quantum field theories, that is, the area law, even in the non-Gaussian regime and for a non-zero temperature. Towards a feasible experimental implementation, we estimate entropic quantities from a finite number of samples without any additional assumptions on the underlying quantum state using k-nearest neighbor estimators.
Y. Deller, M. Gärttner, T. Haas, M. K. Oberthaler, M. Reh, H. Strobel, „Entropy estimation in
a spin-1 Bose-Einstein condensate“, New J. Phys. 27, 043004 (2025).
https://iopscience.iop.org/article/10.1088/1367-2630/adc32a
Related to Project A06
Abstract:
We use the physics-informed renormalisation group (PIRG) for the construction of gauge invariant renormalisation group flows. The respective effective action is a sum of a gauge invariant quantum part and the classical gauge fixing part which arranges for invertibility of the gauge field two-point function. Thus, the BRST transformations simply accommodate the gauge consistency of the gauge fixing sector, while the quantum part of the effective action is gauge and BRST invariant. We apply this physics-informed approach to Yang-Mills theory and gravity and show how the flowing gauge fields arrange for full gauge invariance. We also embed the background field approximation to the functional renormalisation group (fRG) in an exact gauge invariant PIRG flow. This allows us to discuss the dynamics of the correction terms, and the non-trivial ultraviolet or infrared relevant terms are elucidated within a one-loop approximation. The background field approximation of the latter is known for violating one-loop universality for specific regulators and we show how the present setup reinstates universality in a constructive way. Finally, we discuss the landscape of fRG flows in gauge theories through the lens of the novel PIRG approach as well as potential applications.
F. Ihssen, J. M. Pawlowski, „Physics-informed gauge theories“, 28. März 2025, arXiv:2503.
22638 (2025).
https://arxiv.org/abs/2503.22638
Related to Project A02
Abstract:
In the Alphatrap experiment, the 𝑔 factor of boronlike 118Sn45+ has been measured with a 0.5 ppb uncertainty. This is the first high-precision measurement of the 𝑔 factor of a heavy boronlike ion. The measured value of 0.6 447 038 265(4) is consistent with the presented ab initio state-of-the-art theory calculations, which predict a value of 0.64 470 29(8). So far, the only boronlike ion of which the 𝑔 factor was measured with high precision has been 40Ar13+. The measurement presented here therefore tests quantum electrodynamics as well as many-electron interactions at much higher 𝑍. Furthermore, we discuss the potential for an independent determination of the fine-structure constant 𝛼, which can be achieved with a specific difference of 𝑔 factors, combining the presented results with the recent electron 𝑔-factor measurement of hydrogenlike tin.
J. Morgner, B. Tu, M. Moretti, C. M. König, F. HeiSSe, T. Sailer, V. A. Yerokhin, B. Sikora,
N. S. Oreshkina, Z. Harman, C. H. Keitel , S. Sturm , K. Blaum, „g Factor of Boronlike Tin“,
Phys. Rev. Lett. 134, 123201 (2025).
https://journals.aps.org/prl/abstract/10.1103/PhysRevLett.134.123201
Related to Project B01, B02
Abstract:
Systematic expansion schemes in functional approaches require the inclusion of higher order vertices. These vertices are expanded in independent tensor bases with a rapidly increasing number of basis elements. Amongst the related tasks are the construction of bases and projection operators, the importance ordering of their elements, and the optimisation of such tensor bases, as well as an analysis of their regularity in momentum space. We present progress in all these directions and introduce the Mathematica package TensorBases designed for the aforementioned tasks.
J. Braun, A. GeiSSel, J. M. Pawlowski, F. R. Sattler, N. Wink, „Juggling with Tensor Bases in
Functional Approaches“, 7. März 2025, arXiv:2503.05580 (2025).
https://arxiv.org/abs/2503.05580
Related to Project A02
Abstract:
Despite its comparatively low electron affinity, tris(pentafluorophenyl)borane (BCF) has been widely explored as an efficient molecular p-dopant for semiconducting polymers through the formation of Brønsted acidic complexes as well as its high affinity toward Lewis-basic nitrogen moieties. Many conjugated polymers that are used for selective wrapping and dispersion of semiconducting single-walled carbon nanotubes (SWCNTs) such as poly[(9,9-di-n-octylfluorenyl-2,7-diyl)-alt-(6,6′-(2,2′-bipyridine))] (PFO-BPy) contain nitrogen moieties that should promote interaction with BCF. Here, we demonstrate that BCF indeed efficiently p-dopes even small-diameter (6,5) SWCNTs that are wrapped with large-bandgap PFO-BPy as corroborated by bleaching of the main absorption peaks and the appearance of red-shifted trion absorption and emission. In contrast, SWCNTs that are wrapped with poly(9,9-di-n-octylfluorenyl-2,7-diyl) (PFO) without any Lewis-basic nitrogen moieties are only mildly doped. UV–Vis–NIR absorption, 19F NMR, and 11B NMR spectra confirm that BCF dopes the bipyridine-containing PFO-BPy but not PFO, thus leading to a proposed doping mechanism that relies on the unique interactions between BCF, the bipyridine moieties in PFO-BPy, and the nanotubes. Since BCF doping of PFO-BPy-wrapped (6,5) SWCNTs is more efficient than doping with F4TCNQ and more stable than doping with AuCl3, it provides a reliable alternative for spectroscopic studies of the interactions of charge carriers and excitons in SWCNTs.
S. Lindenthal, D. Rippel, L. Kistner, A. Hawkey, J. Zaumseil, „Synergistic p-Doping of Polymer-
Wrapped Small-Diameter Single-Walled Carbon Nanotubes by Tris(pentafluorophenyl)borane“,
J. Phys. Chem. C 129, 5520 (2025).
https://pubs.acs.org/doi/10.1021/acs.jpcc.4c08584
Related to Project C07
Abstract:
We investigate the different degrees of freedom underlying far-from-equilibrium scaling behaviour in a relativistic, single-component O(1) scalar field theory in two and three spatial dimensions. In such a strongly correlated many-body system, identifying the respective roles of nonlinear wave excitations and defect dynamics is a prerequisite for understanding the universal character of time evolution far from equilibrium and thus the different possible universality classes of nonthermal fixed points. Using unequal-time two-point correlation functions, we extract information about the dominant infrared excitations and study their connections to the turbulent dynamics of topological defects created in the system. In three dimensions, the primary excitations are identified as kelvon quasiparticles, which are quantised Kelvin waves propagating along vortex lines, while in two dimensions, vortices are point defects, and the infrared dynamics is dominated by bound-state like excitations similar to Kelvin waves. In both cases, the kelvon excitations are found to be characterised by distinct time-evolving dispersion relations, subject to the coarsening dynamics close to the respective nonthermal fixed point and, thus, to the decay of superfluid turbulence in the system. Our results underline the role of topological defects and their influence on the universal dynamics of strongly correlated systems near nonthermal fixed points, complementing the analysis of large-N models in O(N) systems.
V. Noel, T. Gasenzer, K. Boguslavski, „Kelvin waves in nonequilibrium universal dynamics of
relativistic scalar field theories“, 3. März 2025, arXiv:2503.01771 (2025).
https://arxiv.org/abs/2503.01771
Related to Project A04, B03
Abstract:
In this paper, we develop an approach to calculate the valence-quark quasi parton distribution amplitude (quasi-PDA) and quasi parton distribution function (quasi-PDF) for the pion with a large longitudinal momentum with the functional renormalization group (fRG). This is demonstrated in a low energy effective theory (LEFT) with four-quark scatterings. In the study of the complex structure of quasi-PDA, we introduce a deformed integration contour in the calculations of quasi-PDA or quasi-PDF, which allows us to obtain correct integrals for all momentum fractions. It is found that the pion light-front PDA extrapolated from quasi-PDA based on the large momentum effective theory (LaMET) in the LEFT is comparable with lattice QCD and Dyson-Schwinger equation. This work paves the way to study the PDA and PDF within the fRG approach to first-principles QCD.
D.-y. Zhang, C. Huang, W.-j. Fu, „Quasi parton distributions of pions at large longitudinal
momentum“, 21. Feb. 2025, arXiv:2502.15384 (2025).
https://arxiv.org/abs/2502.15384
Related to Project A02
Abstract:
We study the full infrared dynamics of 2+1 flavour QCD with the functional renormalisation group approach. We resolve self-consistently the glue dynamics as well as the dynamics of chiral symmetry breaking. The computation hosts no phenomenological parameter or external input. The only ultraviolet input parameters are the physical ones in QCD: the light and strange quark masses. They are adjusted to the physical ratios of the pion and kaon masses, divided by the pion decay constant. The results for other observables of current first-principles computations are in quantitative agreement with the physical ones. This work completes the series of papers, initiated and furthered in [1,2], on dynamical chiral symmetry breaking and the emergence of mesonic bound states within the functional renormalisation group. As a first application we discuss the formation of light mesonic bound states. Amongst other applications such as the phase structure of QCD, the current work paves the way for studying QCD parton distribution functions within the functional renormalisation group approach to first-principles QCD.
W.-j. Fu, C. Huang, J. M. Pawlowski, Y.-y. Tan, L.-j. Zhou, „Four-quark scatterings in QCD
III“, 20. Feb. 2025, arXiv:2502.14388 (2025).
https://arxiv.org/abs/2502.14388
Related to Project A02
Abstract:
In this Letter, we present mass-ratio measurements on highly charged Yb42+ ions with a precision of 4 ×10−12 and isotope-shift measurements on Yb+ on the 2S1/2→2D5/2 and 2S1/2→2F7/2 transitions with a precision of 4 ×10−9 for the isotopes 168,170,172,174,176Yb. We present a new method that allows us to extract higher-order changes in the nuclear charge distribution along the Yb isotope chain, benchmarking ab initio nuclear structure calculations. Additionally, we perform a King plot analysis to set bounds on a fifth force in the keV/𝑐2 to MeV/𝑐2 range coupling to electrons and neutrons.
M. Door, C.-H. Yeh, M. Heinz, K. Blaum et al., „Probing New Bosons and Nuclear Structure
with Ytterbium Isotope Shifts“, Phys. Rev. Lett. 134, 063002 (2025).
https://journals.aps.org/prl/abstract/10.1103/PhysRevLett.134.063002
Related to Project B01, B02
Abstract:
Transport in strongly correlated fermions cannot be understood by fermionic quasiparticles alone. We present a theoretical framework for quantum transport that incorporates strong local correlations of fermion pairs. These contact correlations add essential contributions to viscous, thermal and sound transport coefficients. The bulk viscosity, in particular, receives its dominant contribution from pair excitations. Moreover, it can be measured elegantly by observing the response to a time-dependent scattering length even when the fluid is not moving. Rapid changes of the scattering length drive the system far out of local equilibrium, and we show how it relaxes back to equilibrium following a hydrodynamic attractor before a Navier–Stokes description becomes valid. This paper summarizes a talk given at the Symposium “Open questions in the quantum many-body problem” at the Institut Henry Poincaré, Paris, in July 2024.
T. Enss, „Quantum transport in strongly correlated Fermi gases “, Comptes Rendus. Physique 26, 217 (2025).
https://comptes-rendus.academie-sciences.fr/physique/articles/10.5802/crphys.237/
Related to Project ABC, C03
Abstract:
The formation of patterns in driven systems has been studied extensively, and their emergence can be connected to a fine balance of instabilities and stabilization mechanisms. While the early phase of pattern formation can be understood on the basis of linear stability analyses, the longtime dynamics can only be described by accounting for the interactions between the excitations generated by the drive. Here, we observe the stabilization of square patterns in an interaction-driven, two-dimensional Bose-Einstein condensate. These patterns emerge due to inherent high-order processes that become relevant in the regime of large phonon occupations. Theoretically, this can be understood as the emergence of a stable fixed point of coupled nonlinear amplitude equations, which include phonon-phonon interactions. We experimentally probe the predicted flows toward such a stable fixed point, as well as repulsion from a saddle fixed point, using the experimental control unique to quantum gases.
N. Liebster, M. Sparn, E. Kath, K. Fujii, S. Görlitz, T. Enss, H. Strobel, M. K. Oberthaler,
„Observation of Pattern Stabilization in a Driven Superfluid“, Phys. Rev. X 15, 011026 (2025).
https://journals.aps.org/prx/abstract/10.1103/PhysRevX.15.011026
Related to Project C02, C03, A04
Abstract:
An important tool in studying the subfemtoscale spacetime structure of matter in ultrarelativistic heavy-ion collisions is Hanbury Brown–Twiss (HBT) intensity interferometry of identical particles in the final state of the collisions. We propose that a variant of the entanglement enabled intensity interferometry (𝐸2𝐼2) framework introduced by Cotler and Wilczek can provide a powerful alternative to HBT interferometry in extracting fundamental nonperturbative features of quantum chromodynamics at high energies. We apply this framework to demonstrate that the spatial distributions of color singlet (pomeron) configurations in nuclei are sensitive to measurements of exclusive resonant decays of 𝜌 mesons into 𝜋± pairs in ultrarelativistic ultraperipheral nuclear collisions (UPCs) at the Relativistic Heavy Ion Collider and the Large Hadron Collider. A preliminary analysis suggests that the model-independent extraction of pomeron distributions will require careful treatment of the interplay of 𝐸2𝐼2 in the vector meson exclusive decay with the incoherent cross section for exclusive vector meson production. The 𝐸2𝐼2 framework developed here is quite general. It can also be employed as a tool to extract information on the spin structure of pomeron couplings as well as enhance the discovery potential for rare odderon configurations from exclusive vector meson decays into few-particle final states both in UPCs and at the Electron-Ion Collider.
J. D. Brandenburg, H. Duan, Z. Tu, R. Venugopalan, Z. Xu, „Entanglement enabled intensity
interferometry in ultrarelativistic ultraperipheral nuclear collisions“, Phys. Rev. Res. 7, 013131
(2025).
https://journals.aps.org/prresearch/abstract/10.1103/PhysRevResearch.7.013131
Related to Project A01
Abstract:
Symmetries play a pivotal role in our understanding of the properties of quantum many-body systems. While there are theorems and a well-established toolbox for systems in thermal equilibrium, much less is known about the role of symmetries and their connection to dynamics out of equilibrium. This arises due to the direct link between a system’s thermal state and its Hamiltonian, which is generally not the case for nonequilibrium dynamics. Here we present a pathway to identify the effective symmetries and to extract them from data in nonequilibrium quantum many-body systems. Our approach is based on exact relations between correlation functions involving different numbers of spatial points, which can be viewed as nonequilibrium versions of (equal-time) Ward identities encoding the symmetries of the system. We derive symmetry witnesses, which are particularly suitable for the analysis of measured or simulated data at different snapshots in time. To demonstrate the potential of the approach, we apply our method to numerical and experimental data for a spinor Bose gas. We investigate the important question of a dynamical restoration of an explicitly broken symmetry of the Hamiltonian by the initial state. Remarkably, it is found that effective symmetry restoration can occur long before the system equilibrates. We also use the approach to define and identify spontaneous symmetry breaking far from equilibrium, which is of great relevance for applications to nonequilibrium phase transitions. Our work opens new avenues for the classification and analysis of quantum as well as classical many-body dynamics in a large variety of systems, ranging from ultracold quantum gases to cosmology.
A. N. Mikheev, V. Noel, I. Siovitz, H. Strobel, M. K. Oberthaler, J. Berges, „Extracting the
symmetries of nonequilibrium quantum many-body systems“, SciPost Phys. 18, 044 (2025).
https://scipost.org/10.21468/SciPostPhys.18.2.044
Related to Project B04
Abstract:
Hydrodynamic attractors are a universal phenomenon of strongly interacting systems that describe the hydrodynamic-like evolution far from local equilibrium. In particular, the rapid hydrodynamization of the Quark-Gluon Plasma is behind the remarkable success of hydrodynamic models of high-energy nuclear collisions. So far, hydrodynamic attractors have been explored only in systems undergoing monotonic expansion, such as Bjorken flow. We demonstrate that a system with an oscillating isotropic expansion exhibits a novel cyclic attractor behavior. This phenomenon can be investigated in ultracold quantum gases with externally modulated scattering length, offering a new avenue for experimentally discovering hydrodynamic attractors.
A. Mazeliauskas, T. Enss, „Hydrodynamic attractor in periodically driven ultracold quantum
gases“, 31. Jan. 2025, arXiv:2501.19240 (2025).
https://arxiv.org/abs/2501.19240
Related to Project ABC, C03
Abstract:
Conventional hydrodynamics describes systems with few long-lived excitations. In one dimension, however, many experimentally relevant systems feature a large number of long-lived excitations and conserved quantities even at high temperature, because they are proximate to integrable limits. Such models cannot be treated using conventional hydrodynamics. The framework of generalized hydrodynamics (GHD) was recently developed to treat the dynamics of one-dimensional models: It combines ideas from integrability, hydrodynamics, and kinetic theory to come up with a quantitative theory of transport. GHD has successfully settled several long-standing questions about one-dimensional transport; it has also been leveraged to study dynamical questions beyond the transport of conserved quantities and to systems that are not integrable. In this article, we introduce the main ideas and predictions of GHD, survey some of the most recent theoretical extensions and experimental tests of the GHD framework, and discuss some open questions in transport that the GHD perspective might elucidate.
B. Doyon, S. Gopalakrishnan, F. Møller, J. Schmiedmayer, R. Vasseur, „Generalized Hydrodynamics:
A Perspective“, Phys. Rev. X 15, 010501 (2025).
https://journals.aps.org/prx/abstract/10.1103/PhysRevX.15.010501
Related to Project A03
Abstract:
In this work we provide a comprehensive review of theoretical and experimental studies of the properties of polarons formed by mobile impurities strongly interacting with quantum many-body systems. We present a unified perspective on the universal concepts and theoretical techniques used to characterize polarons in two distinct platforms, ultracold atomic gases and atomically-thin transition metal dichalcogenides, which are linked by many deep parallels. We review polarons in both fermionic and bosonic environments, highlighting their similarities and differences including the intricate interplay between few- and many-body physics. Various kinds of polarons with long-range interactions or in magnetic backgrounds are discussed, and the theoretical and experimental progress towards understanding interactions between polarons is described. We outline how polaron physics, regarded as the low density limit of quantum mixtures, provides fundamental insights regarding the phase diagram of complex condensed matter systems. Furthermore, we describe how polarons may serve as quantum sensors of many-body physics in complex environments. Our work highlights the open problems, identifies new research directions and provides a comprehensive framework for this rapidly evolving research field.
P. Massignan, R. Schmidt, G. E. Astrakharchik, A. Imamoglu, M. Zwierlein, J. J. Arlt, G.
M. Bruun, „Polarons in atomic gases and two-dimensional semiconductors“, 16. Jan. 2025,
arXiv:2501.09618 (2025).
https://arxiv.org/abs/2501.09618
Related to Project C01
Abstract:
We report on the development of a modular platform for programmable quantum simulation with atomic quantum gases. The platform is centered around exchangeable optical modules with versatile functionalities. The performance of each module is disentangled from all others, enabling individual validation and maintenance of its outputs. The relative spatial positioning of the modules with respect to the position of the atomic sample is set by a global reference frame. In this way, the platform simplifies re-configuration and upgrading of existing setups and accelerates the design of new machines in a time- and cost-efficient manner. Furthermore, it facilitates collaboration among different experimental groups. This standardized hardware design framework, which we call Heidelberg Quantum Architecture, paves the way towards a new generation of on-demand and highly adaptable quantum simulation experiments.
T. Hammel, M. Kaiser, D. Dux, P. M. Preiss, M. Weidemüller, S. Jochim, „A modular quantum
gas platform“, 14. Jan. 2025, arXiv:2501.08211 (2025).
https://arxiv.org/abs/2501.08211
Related to Project A05
Abstract:
We engineer angular momentum eigenstates of a single atom by using a novel all-optical approach based on the interference of Laguerre-Gaussian beams. We confirm the imprint of angular momentum by measuring the two-dimensional density distribution and by performing Ramsey spectroscopy in a slightly anisotropic trap, which additionally reveals the sense of rotation. This article provides the experimental details on the quantum state control of angular momentum eigenstates reported in P. Lunt et al., Phys. Rev. Lett. 133, 253401 (2024).
P. Lunt, P. Hill, J. Reiter, P. M. Preiss, M. Galka, S. Jochim, „Engineering single-atom angular
momentum eigenstates in an optical tweezer“, 13. Jan. 2025, arXiv:2501.07414 (2025).
https://arxiv.org/abs/2501.07414
Related to Project C02
Abstract:
We study the time evolution of a state of a relativistic quantum field theory restricted to a spatial subregion Ω. More precisely, we use the Feynman-Vernon influence functional formalism to describe the dynamics of the field theory in the interior of Ω arising after integrating out the degrees of freedom in the exterior. We show how the influence of the environment gets encoded in a boundary term. Furthermore, we derive a stochastic equation of motion for the field expectation value in the interior. We find that the boundary conditions obtained in this way are energy nonconserving and nonlocal in space and time. Our results find applications in understanding the emergence of local thermalization in relativistic quantum field theories and the relationship between quantum field theory and relativistic fluid dynamics.
M. Schröfl, S. Floerchinger, „Time evolution of relativistic quantum fields in spatial subregions“,
Phys. Rev. D 111, 025009 (2025).
https://journals.aps.org/prd/abstract/10.1103/PhysRevD.111.025009
Related to Project A06, C06
Abstract:
Hydrodynamics is a successful framework for effectively describing the dynamics of complex many-body systems, ranging from subnuclear to cosmological scales. It applies coarse-grained assumptions about the microscopic constituents of a system to define macroscopic fluid cells, which are large compared to the interparticle spacing and mean free path. In high-energy heavy-ion collisions, hydrodynamic behaviour is inferred from the observation of elliptic flow, which is the elliptical deformation of the particle momentum distribution. Here we demonstrate the emergence of elliptic flow in a mesoscopic system with a few strongly interacting ultracold atoms. In our system, a hydrodynamic description is a priori not applicable, as all relevant length scales—the system size, the interparticle spacing and the mean free path—are comparable. The single-particle resolution and the deterministic control over the number of particles and interaction strength in our experiment allow us to explore the boundaries between a microscopic description and a hydrodynamic framework, and we show that elliptic flow appears as an interaction-driven effect. Our results demonstrate the emergence of collective behaviour in a regime where hydrodynamics is not usually applicable.
S. Brandstetter, P. Lunt, C. Heintze, G. Giacalone, L. H. Heyen, M. Galka, K. Subramanian,
M. Holten, P. M. Preiss, S. Floerchinger, S. Jochim, „Emergent interaction-driven elliptic flow
of few fermionic atoms“, Nat. Phys. 21, 52 (2025).
https://www.nature.com/articles/s41567-024-02705-8
Related to Project ABC, C01, C02, C06
Abstract:
We experimentally study cosmological particle production in a two-dimensional Bose-Einstein condensate, whose density excitations map to an analog cosmology. The expansion of spacetime is realized with tunable interactions. The particle spectrum can be understood through an analogy to quantum mechanical scattering, in which the dynamics of the spacetime metric determine the shape of the scattering potential. Hallmark scattering phenomena such as resonant forward scattering and Bragg reflection are connected to their cosmological counterparts, namely linearly expanding space and bouncing universes. We compare our findings to a theoretical description that extends beyond the acoustic approximation, which enables us to apply the model to high-momentum excitations.
M. Sparn, E. Kath, N. Liebster, J. Duchene, C.F. Schmidt, M. Tolosa-Simeón, Á. Parra-López,
S. Floerchinger, H. Strobel, M. K. Oberthaler, „Experimental Particle Production in Time-
Dependent Spacetimes: A One-Dimensional Scattering Problem“, Phys. Rev. Lett. 133, 260201
(2024).
https://journals.aps.org/prl/abstract/10.1103/PhysRevLett.133.260201
Related to Project A04
Abstract:
We compute meson spectral functions at finite temperature and density in the quark-meson model, supplemented with a computation of the phase diagram. In particular, we provide a detailed analysis of the non-analytic structure of the meson two-point functions which is of great relevance for phenomenological applications, such as moat regimes and inhomogeneous phases. Furthermore, it is also relevant from a field-theoretical standpoint as it provides an insight into the applicability of derivative expansions of the effective action to studies of general fermion-boson models, both at zero and finite chemical potential. Our computation is based on a functional renormalization group setup that preserves causality, all spacetime symmetries, and the Silver-Blaze property. The combination of these properties can only be achieved by a Callan-Symanzik regulator. Instead of momentum shell integrations, renormalization group flows generated by such a regulator describe the change of the theory induced by a change of the masses of the mesons and quarks. A particular focus of our work lies on the construction of controlled Callan-Symanzik flows in the presence of spontaneous and explicit chiral symmetry breaking by means of chiral Ward-Takahashi identities.
S. Töpfel, J. M. Pawlowski, J. Braun, „Phase structure of quark matter and in-medium properties
of mesons from Callan-Symanzik flows“, 20. Dez. 2024, arXiv:2412 . 16059 (2025).
https://arxiv.org/abs/2412.16059
Related to Project A02
Abstract:
The identity method is a statistical technique developed to reconstruct moments of multiplicity distributions of particles produced in high-energy nuclear collisions. The method leverages principles from fuzzy logic, allowing for a more nuanced representation of particle identification by assigning degrees of membership to different particle types based on detector signals. In this contribution, a new framework, based on a multivariate moment generating function, is developed that allows the derivation of the formulas used in the identity method in a more robust way. Moreover, within the introduced framework, the identity method is easily extended to cope with arbitrarily higher-order moments. The techniques developed here offer significant potential for improving the accuracy of multiplicity distribution analyses in high-energy nuclear collisions. While the primary focus of the work presented is on applications in high-energy particle and nuclear physics, it can also be applied in other areas where signal identification is probabilistic and data are noisy, such as in medical imaging, remote sensing, and various other fields of experimental science.
A. Rustamov, „Fuzzy logic for reconstructing arbitrary moments of multiplicity distributions“,
Phys. Rev. C 110, 064910 (2024).
https://journals.aps.org/prc/abstract/10.1103/PhysRevC.110.064910
Related to Project A01
Abstract:
Far from equilibrium, universal dynamics prevails in many different situations, from pattern coarsening to turbulence, while the understanding of its microscopic laws and classification has remained unsatisfactory. Here, universal scaling evolution reflected by coarsening in a multi-component Bose gas is traced back to a low-energy effective theory given by a double sine-Gordon (DSG) model for a single real scalar field. Our experimental observations of a rubidium spinor BEC support the applicability of this model. Evaluating the scaling evolution according to the low-energy effective model demonstrates the universal aspects of the scaling characteristics as compared with that of the spinor gas. The difference between diffusion-type and sub-diffusive scaling is shown to be connected to the occupation of minima within the DSG potential. Our results point to a path towards a microscopic description and classification of pattern coarsening in many-body systems.
I. Siovitz, A.-M. E. Glück, Y. Deller, A. Schmutz, F. Klein, H. Strobel, M. K. Oberthaler, T.
Gasenzer, „Double sine-Gordon class of universal coarsening dynamics in a spin-1 Bose gas“,
18. Dez. 2024, arXiv:2412.13986 (2024).
https://arxiv.org/abs/2412.13986
Related to Project A04
Abstract:
This report summarizes the work of the EMMI Rapid Reaction Task Force on “Real and Virtual Photon Production at Ultra-Low Transverse Momentum and Low Mass at the LHC”. We provide an overview of the soft-photon puzzle, i.e., of the long-standing discrepancy between experimental data and predictions based on Low’s soft-photon theorem, also referred to as “anomalous” soft photon production, and we review the current theoretical understanding of soft radiation and soft theorems. We also focus on low-mass dileptons as a tool for determining the electrical conductivity of the medium produced in high-energy nucleus–nucleus collisions. We discuss how both topics can be addressed with the planned ALICE 3 detector at the LHC.
R. Bailhache et al., „Anomalous soft photons: Status and perspectives“, Phys. Rep. 1097, 1 (2024).
https://www.sciencedirect.com/science/article/pii/S0370157324003478
Related to Project A01
Abstract:
We realize a Laughlin state of two rapidly rotating fermionic atoms in an optical tweezer. By utilizing a single atom and spin resolved imaging technique, we sample the Laughlin wave function thereby revealing its distinctive features, including a vortex distribution in the relative motion, correlations in the particles’ relative angle, and suppression of the interparticle interactions. Our Letter lays the foundation for atom-by-atom assembly of fractional quantum Hall states in rotating atomic gases.
P. Lunt, P. Hill, J. Reiter, P. M. Preiss, M. Galka, S. Jochim, „Realization of a Laughlin State
of Two Rapidly Rotating Fermions“, Phys. Rev. Lett. 133, 253401 (2024).
https://journals.aps.org/prl/abstract/10.1103/PhysRevLett.133.253401
Related to Project C01
Abstract:
Quantum field theories (QFTs) as relevant for condensed-matter or high-energy physics are formulated in continuous space and time, and typically emerge as effective low-energy descriptions. In atomic physics, an example is given by tunnel-coupled superfluids, which realize the paradigmatic sine-Gordon model, and can act as quantum simulators of continuous QFTs. To quantitatively characterize QFT simulators, or to discover the Hamiltonian governing the dynamics of a continuous many-body quantum system, we discuss Hamiltonian learning as a method to systematically extract the operator content and the coupling constants of Hamiltonians from experimental data. In contrast to Hamiltonian learning for lattice models with a given lattice scale, we learn QFT Hamiltonians on a resolution scale set by the experiment. Varying the resolution scale gives access to QFTs at different energy scales, and allows to learn a flow of Hamiltonians reminiscent of the renormalization group. Applying these techniques to available experimental data from a tunnel-coupled quantum gas experiment allows a definite distinction between a free quadratic theory from an interacting sine-Gordon model, as the underlying QFT description of the system.
R. Ott, T. V. Zache, M. Prüfer, S. Erne, M. Tajik, H. Pichler, J. Schmiedmayer, P. Zoller,
„Hamiltonian learning in quantum field theories“, Phys. Rev. Res. 6, 043284 (2024).
https://journals.aps.org/prresearch/abstract/10.1103/PhysRevResearch.6.043284
Related to Project A03
Abstract:
The production of quantum field excitations or particles in cosmological spacetimes is a hallmark prediction of curved quantum field theory. The generation of cosmological perturbations from quantum fluctuations in the early Universe constitutes an important application. The problem can be quantum-simulated in terms of structure formation in an interacting Bose-Einstein condensate (BEC) with time-dependent s-wave scattering length. Here, we explore a mapping between cosmological particle production in general (𝐷+1)-dimensional spacetimes and scattering problems described by the nonrelativistic stationary Schrödinger equation in one dimension. Through this mapping, intuitive explanations for emergent spatial structures in both the BEC and the cosmological system can be obtained for analogue cosmological scenarios that range from power-law expansions to periodic modulations. The investigated cosmologies and their scattering analogs are tuned to be implemented in a (2+1)-dimensional quantum field simulator.
C. F. Schmidt, Á. Parra-López, M. Tolosa-Simeón, M. Sparn, E. Kath, N. Liebster, J. Duchene,
H. Strobel, M. K. Oberthaler, S. Floerchinger, „Cosmological particle production in a quantum
field simulator as a quantum mechanical scattering problem“, Phys. Rev. D 110, 123523 (2024).
https://journals.aps.org/prd/abstract/10.1103/PhysRevD.110.123523
Related to Project A04
Abstract:
We conduct a numerical study of relativistic viscous fluid dynamics in the Density Frame for one-dimensional fluid flows. The Density Frame is a formulation of relativistic viscous hydrodynamics that is first-order in time, requires no auxiliary fields, and has no non-hydrodynamic modes. We compare our results to QCD kinetic theory simulations and find excellent agreement within the regime of applicability of hydrodynamics. Additionally, the Density Frame results remain well-behaved and robust near the boundary of applicability. We also compare our findings to the second-order-in-time hydrodynamic theory developed by Bemfica, Disconzi, Noronha, and Kovtun (BDNK) and a well-known Müller-Israel-Stewart-type hydrodynamics code, MUSIC, which is commonly used to simulate heavy-ion collisions.
J. Bhambure, A. Mazeliauskas, J.-F. Paquet, R. Singh, M. Singh, D. Teaney, F. Zhou, „Relativistic
Viscous Hydrodynamics in the Density Frame: Numerical Tests and Comparisons“,
13. Dez. 2024, arXiv:2412.10303 (2024).
https://arxiv.org/abs/2412.10303
Related to Project A01
Abstract:
The functional determinant approach (FDA) is a simple method to compute exactly certain observables for ideal quantum systems and has been successfully applied to the Fermi polaron problem to obtain the dynamical overlap and spectral function. Unfortunately, its application to bosonic ultracold gases is prohibited by the failure of the grand canonical ensemble for these systems. In this paper we show how to circumvent this problem and develop a bosonic FDA. This yields exact injection and ejection spectra for ideal Bose polarons at arbitrary temperatures. While coherent features visible at absolute zero quickly smear out with rising temperature as expected, the linewidth of the main peak is, counterintuitively, found to decrease near unitarity. Furthermore, we provide explicit formulas for the overlap operator, which allow us to compute the necessary determinants for both Bose and Fermi polarons more efficiently than previously possible.
M. Drescher, M. Salmhofer, T. Enss, „Bosonic functional determinant approach and its application
to polaron spectra“, Phys. Rev. A 110, 063303 (2024).
https://journals.aps.org/pra/abstract/10.1103/PhysRevA.110.063303
Related to Project C03, C02
Abstract:
In [SciPost Phys. 14, 069 (2023)], we initiated a program for the quantitative investigation of dynamical chiral symmetry breaking and resonant bound states in QCD with the functional renormalisation group, concentrating on the full infrared dynamics of four-quark scatterings. In the present work we extend this study and take into account a three-momentum channel approximation (-channel) for the Fierz-complete four-quark vertices. We find that the four-quark vertex in this approximation is quantitatively reliable. In particular, we have computed the pion pole mass, pion decay constant, Bethe-Salpeter amplitudes, the quark mass function and wave function. Our results confirm previous findings that low energy effective theories only reproduce QCD quantitatively, if initiated with a relatively low ultraviolet cutoff scale of the order of 500 MeV. The quantitative description set up here paves the way for reliable quantitative access to the resonance structure in QCD within the fRG approach to QCD.
W.-j. Fu, C. Huang, J. M. Pawlowski, Y.-y. Tan, „Four-quark scatterings in QCD II“, SciPost
Phys. 17, 148 (2024).
https://scipost.org/10.21468/SciPostPhys.17.5.148
Related to Project A02, B03, C01
Abstract:
We present the experimental apparatus enabling the observation of the heteronuclear Efimov effect in an optically trapped ultracold mixture of ^{6}Li-^{133}Cs with high-resolution control of the interactions. A compact double-species Zeeman slower consisting of four interleaving helical coils allows for a fast-switching between two optimized configurations for either Li or Cs and provides an efficient sequential loading into their respective MOTs. By means of a bichromatic optical trapping scheme based on species-selective trapping we prepare mixtures down to 100 nK of 1 x 10^4 Cs atoms and 7 x 10^3 Li atoms. Highly stable magnetic fields allow high-resolution atom-loss spectroscopy and enable to resolve splitting in the loss feature of a few tens of milligauss. These features allowed for a detailed study of the Efimov effect.
E. Lippi, M. Gerken, S. Häfner, M. Repp, R. Pires, M. Rautenberg, T. Krom, E. D. Kuhnle, B.
Tran, J. Ulmanis, L. Chomaz, M. Weidemüller, „An Experimental Platform for Studying the
Heteronuclear Efimov Effect with an Ultracold Mixture of 6Li and 133Cs Atoms“, Few-Body
Syst 66, 1 (2024).
https://link.springer.com/article/10.1007/s00601-024-01971-9
Related to Project C03
Abstract:
Transverse momentum pT spectra and anisotropic flow distributions are studied for charmonia and charmed hadrons produced in Pb-Pb collisions and measured with the ALICE detector at the CERN Large Hadron Collider (LHC). The investigations are performed within the framework of the Statistical Hadronization Model with the transverse dynamics evaluated using predictions from relativistic viscous hydrodynamics as implemented in the computer codes MUSIC and FluiduM. With this essentially parameter-free approach good agreement is obtained for pT spectra in the range pT < 10 GeV/c. The observed wide distribution in pT of anisotropic flow coefficients v2 and v3 for charmonia is also well reproduced, while their magnitude is generally somewhat over predicted. This finding may be connected to a difference in spatial distribution between light and charmed hadrons due to a different diffusion of light and heavy quarks in the hot fireball.
A. Andronic, P. Braun-Munzinger, H. Brunssen, J. Crkovská, J. Stachel, V. Vislavicius, M.
Völkl, „Transverse dynamics of charmed hadrons in ultra-relativistic nuclear collisions“, JHEP
10, 229 (2024).
https://link.springer.com/article/10.1007/JHEP10(2024)229
Related to Project A01, A02, C06, C05
Abstract:
The hydrodynamic attractor is a concept that describes universal equilibration behavior in which systems lose microscopic details before hydrodynamics becomes applicable. We propose a setup to observe hydrodynamic attractors in ultracold atomic gases, taking advantage of the fact that driving the two-body 𝑠-wave scattering length causes phenomena equivalent to isotropic fluid expansions. We specifically consider two-component fermions with contact interactions in three dimensions and discuss their dynamics under a power-law drive of the scattering length in a uniform system. By explicit computation, we derive a hydrodynamic relaxation model. We analytically solve their dynamics and find the hydrodynamic attractor solution. Our proposed method using the scattering length drive is applicable to a wide range of ultracold atomic systems, and our results establish these as a new platform for exploring hydrodynamic attractors.
K. Fujii, T. Enss, „Hydrodynamic Attractor in Ultracold Atoms“, Phys. Rev. Lett. 133, 173402 (2024).
https://journals.aps.org/prl/abstract/10.1103/PhysRevLett.133.173402
Related to Project C02, C06, ABC
Abstract:
We generalize and extend the recently proposed method [1] to account for contributions of system size (or volume/participant) fluctuations to the experimentally measured moments of particle multiplicity distributions. We find that in the general case there are additional biases which are not directly accessible to experiment. These biases are, however, parametrically suppressed if the multiplicity of the particles of interest is small compared to the total charged-particle multiplicity, e.g., in the case of proton number fluctuations at top RHIC and LHC energies. They are also small if the multiplicity distribution of charged particles per wounded nucleon is close to the Poissonian limit, which is the case at low energy nuclear collisions, e.g., at GSI/SIS18. We further find that mixed events are not necessarily needed to extract the correction for volume fluctuations. We provide the formulas to correct pure and mixed cumulants of particle multiplicity distributions up to any order together with their associated biases.
R. Holzmann, V. Koch, A. Rustamov, J. Stroth, „Controlling volume fluctuations for studies of
critical phenomena in nuclear collisions“, Nucl. Phys. A 1050, 122924 (2024).
https://www.sciencedirect.com/science/article/pii/S0375947424001064
Related to Project A01
Abstract:
We extend the QCD Parton Model analysis using a factorized nuclear structure model incorporating individual nucleons and pairs of correlated nucleons. Our analysis of high-energy data from lepton deep-inelastic scattering, Drell-Yan, and 𝑊 and 𝑍 boson production simultaneously extracts the universal effective distribution of quarks and gluons inside correlated nucleon pairs, and their nucleus-specific fractions. Such successful extraction of these universal distributions marks a significant advance in our understanding of nuclear structure properties connecting nucleon- and parton-level quantities.
A. W. Denniston, T. Jezo, A. Kusina, N. Derakhshanian, P. Duwentaster, O. Hen, C. Keppel, M.
Klasen, K. Kovarik, J.G. Morfin, K.F. Muzakka, F.I. Olness, E. Piasetzky, P. Risse, R. Ruiz,
I. Schienbein, J.Y. Yu, „Modification of Quark-Gluon Distributions in Nuclei by Correlated
Nucleon Pairs“, Phys. Rev. Lett. 133, 152502 (2024).
https://journals.aps.org/prl/abstract/10.1103/PhysRevLett.133.152502
Related to Project C05
Abstract:
We theoretically investigate the impact of weak static perturbations of a flat potential on the density of a quasi-two-dimensional dipolar Bose gas. We consider the perturbative effects of potential perturbations at first order and restrict to the mean-field stable regime. We first study cosinusoidal potential perturbations at a given spatial frequency; this allows us to understand the effects of optical lattices as well as of isolated momentum contributions in the Fourier decomposition of an arbitrary potential. We then study potential perturbations characterized by a static white-noise spectrum over a given momentum range; this captures the effects of inherent optical aberrations in setups that create uniform optical dipole traps.
T. Bourgeois, L. Chomaz, „Effect of trap imperfections on the density of a quasi-two-dimensional
uniform dipolar quantum Bose gas“, Phys. Rev. A 110, 043303 (2024).
https://journals.aps.org/pra/abstract/10.1103/PhysRevA.110.043303
Related to Project A07
Abstract:
Understanding many body systems is a key challenge in physics. Single atom resolved imaging techniques have unlocked access to microscopic correlations in ultracold quantum gases. However they cannot be used when the relevant length scales are obscured by the resolution of the detection technique. We present a matterwave magnification scheme, based on evolutions in optical potentials, tailored to magnify the wave function of atoms, such that all length scales can be resolved. To showcase this method, we image atoms in the strongly interacting regime, establishing a new way to characterize correlated systems.
S. Brandstetter, C. Heintze, K. Subramanian, P. Hill, P. M. Preiss, M. Galka, S. Jochim,
„Magnifying the Wave Function of Interacting Fermionic Atoms“, 27. Sep. 2024, arXiv:2409.18954 (2024).
https://www.arxiv.org/abs/2409.18954
Related to Project ABC, C01
Abstract:
Wilson’s renormalization-group approach to the weakly-interacting single-component Bose gas is discussed within the symmetry-broken, condensate phase. Extending upon the work by Bijlsma and Stoof, wave-function renormalization of the temporal derivative contributions to the effective action is included in order to capture sound-like quasiparticle excitations with wave lengths larger than the healing-length scale. By means of a suitable rescaling scheme we achieve convergence of the coupling flows, which serve as a means to determine the condensate depletion in accordance with Bogoliubov theory, as well as the interaction-induced shift of the critical temperature.
N. Rasch, A. N. Mikheev, T. Gasenzer, „Bogoliubov phonons in a Bose-Einstein condensate from
the one-loop perturbative renormalization group“, SciPost Phys. Core 7, 066 (2024).
https://www.scipost.org/SciPostPhysCore.7.3.066
Related to Project A04
Abstract:
Off-shell effects in large LHC backgrounds are crucial for precision predictions and, at the same time, challenging to simulate. We present a novel method to transform high-dimensional distributions based on a diffusion neural network and use it to generate a process with off-shell kinematics from the much simpler on-shell one. Applied to a toy example of top pair production at LO we show how our method generates off-shell configurations fast and precisely, while reproducing even challenging on-shell features.
A. Butter, T. Jezo, M. Klasen, M. Kuschick, S. P. Schweitzer, T. Plehn, „Kicking it off(-shell)
with direct diffusion“, SciPost Phys. Core 7, 064 (2024).
https://scipost.org/10.21468/SciPostPhysCore.7.3.064
Related to Project C05
Abstract:
We formulate the induced potential in a finite-temperature cold-atomic medium between two heavy impurities, or polarons, which is shown to be complex valued in general. The imaginary part of the complex-valued potential describes a decoherence effect, and thus the resulting Schrödinger equation for the two polarons acquires a non-Hermitian term. We apply the developed formulation to two representative cases of polarons interacting with medium particles through the 𝑠-wave contact interaction: (i) the normal phase of single-component (i.e., spin-polarized) fermions using the fermionic field theory and (ii) a superfluid phase using the superfluid effective field theory, which is valid either for a Bose-Einstein condensate (BEC) of a single-component Bose gas or for the BEC-BCS crossover in two-component fermions at a low-energy regime. Computing the leading-order term, the imaginary part of the potential in both cases is found to show a universal 𝑟−2 behavior at long distance. We propose three experimental ways to observe the effects of the universal imaginary potential in cold atoms.
Y. Akamatsu, S. Endo, K. Fujii, M. Hongo, „Complex-valued in-medium potential between heavy impurities in ultracold atoms“, Phys. Rev. A 110, 033304 (2024).
https://journals.aps.org/pra/abstract/10.1103/PhysRevA.110.033304
Related to Project C02, C03
Abstract:
Time reversal in a macroscopic system contradicts daily experience. It is practically impossible to restore a shattered cup to its original state by just time reversing the microscopic dynamics that led to its breakage. Yet, with the precise control capabilities provided by modern quantum technology, the unitary evolution of a quantum system can be reversed in time. Here, we implement a time-reversal protocol in a dipolar interacting, isolated many-body spin system represented by Rydberg states in an atomic gas. By changing the states encoding the spin, we flip the sign of the interaction Hamiltonian, and demonstrate the reversal of the relaxation dynamics of the magnetization by letting a demagnetized many-body state evolve back in time into a magnetized state. We elucidate the role of atomic motion using the concept of a Loschmidt echo. Finally, by combining the approach with Floquet engineering, we demonstrate time reversal for a large family of spin models with different symmetries. Our method of state transfer is applicable across a wide range of quantum simulation platforms and has applications far beyond quantum many-body physics, reaching from quantum-enhanced sensing to quantum information scrambling.
S. Geier, A. Braemer, E. Braun, M. Müllenbach, T. Franz, M. Gärttner, G. Zürn, M. Weidemüller,
„Time-reversal in a dipolar quantum many-body spin system“, Phys. Rev. Res. 6, 033197 (2024).
https://journals.aps.org/prresearch/abstract/10.1103/PhysRevResearch.6.033197
Related to Project A05
Abstract:
We present a comprehensive numerical investigation of the cluster truncated Wigner approximation (cTWA) applied to quench dynamics in bond-disordered Heisenberg spin chains with power-law interactions. We find that cTWA yields highly accurate results over a wide parameter range. However, its accuracy hinges on a suitable choice of clusters. By using a clustering strategy inspired by the strong disorder renormalization group and real-space renormalization group (RSRG), clusters of two spins are sufficient to obtain essentially exact results in the regime of strong disorder. Surprisingly, even for rather weak disorder, e.g., in the presence of very long-range interactions, this choice of clustering outperforms a naive choice of clusters of consecutive spins. Additionally, we develop a discrete sampling scheme for the initial Wigner function, as an alternative to the originally introduced scheme based on Gaussian approximations. This sampling scheme puts cTWA on the same conceptional footing as regular discrete TWA for single spins and yields some reduction in the Monte Carlo shot noise compared to the Gaussian scheme.
A. Braemer, J. Vahedi, M. Gärttner, „Cluster truncated Wigner approximation for bonddisordered Heisenberg spin models“, Phys. Rev. B 110, 054204 (2024).
https://journals.aps.org/prb/abstract/10.1103/PhysRevB.110.054204
Related to Project A05
Abstract:
The ALICE experiment was proposed in 1993, to study strongly-interacting matter at extreme energy densities and temperatures. This proposal entailed a comprehensive investigation of nuclear collisions at the LHC. Its physics programme initially focused on the determination of the properties of the quark–gluon plasma (QGP), a deconfined state of quarks and gluons, created in such collisions. The ALICE physics programme has been extended to cover a broader ensemble of observables related to Quantum Chromodynamics (QCD), the theory of strong interactions. The experiment has studied Pb–Pb, Xe–Xe, p–Pb and pp collisions in the multi-TeV centre of mass energy range, during the Run 1–2 data-taking periods at the LHC (2009–2018). The aim of this review is to summarise the key ALICE physics results in this endeavor, and to discuss their implications on the current understanding of the macroscopic and microscopic properties of strongly-interacting matter at the highest temperatures reached in the laboratory. It will review the latest findings on the properties of the QGP created by heavy-ion collisions at LHC energies, and describe the surprising QGP-like effects in pp and p–Pb collisions. Measurements of few-body QCD interactions, and their impact in unraveling the structure of hadrons and hadronic interactions, will be discussed. ALICE results relevant for physics topics outside the realm of QCD will also be touched upon. Finally, prospects for future measurements with the ALICE detector in the context of its planned upgrades will also be briefly described.
ALICE Collaboration, S. Acharya, D. Adamová et al., „The ALICE experiment: a journey
through QCD“, Eur. Phys. J. C 84, 813 (2024).
https://link.springer.com/article/10.1140/epjc/s10052-024-12935-y
Related to Project A01, A02, C05, C06
Abstract:
The study of event-by-event fluctuations of net-baryon number in a subspace of full phase space is a promising direction for deciphering the structure of strongly interacting matter created in collisions of relativistic heavy nuclei. Such fluctuations are generally suppressed by exact baryon number conservation. Moreover, the suppression is stronger if baryon number is conserved locally. In this report we present a conceptually new approach to quantify correlations in rapidity space between baryon-antibaryon, baryon-baryon, and antibaryon-antibaryon pairs and demonstrate their impact on net-baryon number fluctuations. For the special case of Gaussian rapidity distributions, we use the Cholesky factorization of the covariance matrix, while the general case is introduced by exploiting the well-known Metropolis and Simulated Annealing methods. The approach is based on the use of the canonical ensemble of statistical mechanics for baryon number and can be applied to study correlations between baryons as well as strange and/or charm hadrons. It can also be applied to describe relativistic nuclear collisions leading to the production of multi-particle final states. One application of our method is the search for formation of proton clusters at low collision energies emerging as a harbinger of the anticipated first-order chiral phase transition. In a first step, the results obtained are compared to the recent measurements from the CERN ALICE collaboration. Such investigations are key to explore the phase diagram of strongly interacting matter and baryon production mechanisms at energy scales from several GeV to several TeV.
P. Braun-Munzinger, K. Redlich, A. Rustamov, J. Stachel, „The imprint of conservation laws on correlated particle production“, JHEP 2024, 113 (2024).
https://link.springer.com/article/10.1007/JHEP08(2024)113
Related to Project C05
Abstract:
We consider a scalar quantum field theory with global 𝑂(𝑁)3 symmetry in four Euclidean dimensions and solve it numerically in closed form in the large-𝑁 limit. For imaginary tetrahedral coupling the theory is asymptotically free, with stable and real quantum effective action. We demonstrate the dynamical build-up of a strong interaction as the correlation length increases in a regime where the coupling renormalization flow remains well defined in the infrared. This is in contrast to perturbative results of asymptotically free theories, which predict that the coupling becomes ill defined in the infrared, like in quantum chromodynamics. These properties make the model an important laboratory for the study of strong-coupling phenomena in quantum field theory from first principles.
J. Berges, R. Gurau, H. Keppler, T. Preis, „Coupling renormalization flow in the strongly
interacting regime of an asymptotically free quantum field theory in four dimensions“, Phys.
Rev. D 110, 036007 (2024).
https://journals.aps.org/prd/abstract/10.1103/PhysRevD.110.036007
Related to Project B03, B04
Abstract:
We study the QCD equation of state and other thermodynamic observables including the isentropic trajectories and the speed of sound. These observables are of eminent importance for the understanding of experimental results in heavy ion collisions and also provide a QCD input for studies of the timeline of heavy-ion-collisions with hydrodynamical simulations. They can be derived from the quark propagator whose gap equation is solved within a minimal approximation to the Dyson-Schwinger equations (DSEs) of QCD at finite temperature and density. This minimal approximation aims at a combination of computational efficiency and simplification of the truncation scheme while maintaining quantitative precision. This minimal DSE scheme is confronted and benchmarked with results for correlation functions and observables from lattice QCD at vanishing density and quantitative functional approaches at finite density.
Y. Lu, F. Gao, Y.-X. Liu, J. M. Pawlowski, „QCD equation of state and thermodynamic
observables from computationally minimal Dyson-Schwinger equations“, Phys. Rev. D 110, 014036 (2024).
https://journals.aps.org/prd/abstract/10.1103/PhysRevD.110.014036
Related to Project A02, B03, C01
Abstract:
To maximise the information obtained from various independent new physics searches conducted at the LHC, it is imperative to consider the combination of multiple analyses. To showcase the exclusion power gained by combining signal regions from different searches, we consider a simplified scenario inspired by supersymmetry, with all particles but one squark flavour and a bino-like neutralino decoupled. The corresponding signal therefore comprises strong squark pair production, associated squark-neutralino production, as well as weak neutralino pair production. We find that considering the associated and strong production mechanisms together significantly impacts mass limits, while contributions from the weak production are insignificant in the context of current exclusion limits. In addition, we demonstrate that the combination of uncorrelated signal regions as assessed from the recent TACO approach substantially pushes exclusion limits towards higher masses, relative to the bounds derived from the most sensitive individual analyses.
A. Feike, J. Fiaschi, B. Fuks, M. Klasen, A. P. Neuwirth, „Combination and reinterpretation of LHC SUSY searches“, JHEP 2024, 122 (2024).
https://link.springer.com/article/10.1007/JHEP07(2024)122
Related to Project C05
Abstract:
We study the energy deposition and thermalisation of high-momentum on-shell partons (minijets) travelling through a non-equilibrium Quark-Gluon Plasma using QCD kinetic theory. For thermal backgrounds, we show that the parton energy first flows to the soft sector by collinear cascade and then isotropises via elastic scatterings. In contrast, the momentum deposition from a minijet reaches the equilibrium distribution directly. For expanding non-equilibrium QGP, we study the time for a minijet perturbation to lose memory of its initial conditions, namely, the hydrodynamisation time. We show that the minijet evolution scales well with the relaxation time τR ∝ η/s/T(τ), where T(τ) is the effective temperature and η/s is the viscosity over entropy ratio.
F. Zhou, J. Brewer, A. Mazeliauskas, „Minijet quenching in non-equilibrium quark-gluon plasma“,
JHEP 2024, 214 (2024).
https://link.springer.com/article/10.1007/JHEP06(2024)214
Related to Project A01
Abstract:
I review developments of how compact table-top setups with ultracold atoms can help us to understand the more complex real-time dynamics of QCD probed in heavy-ion collision experiments.
J. Berges, „What ultracold atoms tell us about the real-time dynamics of QCD in extreme conditions“, EPJ Web Conf. 296, 01021 (2024).
Related to Project A01, A02, A03, A04, B03, B04, C02, C06
Abstract:
Nuclear collisions at sufficiently high energies are expected to produce far-from-equilibrium matter with a high density of gluons at early times. We show gauge condensation, which occurs as a consequence of the large density of gluons. To identify this condensation phenomenon, we construct two local gauge invariant observables that carry the macroscopic zero mode of the gauge condensate. The first order parameter for gauge condensation investigated here is the correlator of the spatial Polyakov loop. We also consider, for the first time, the correlator of the gauge invariant scalar field, associated with the exponent of the Polyakov loop. Using real-time lattice simulations of classical-statistical SU(2) gauge theory, we find gauge condensation on a system-size-dependent timescale 𝑡cond∼𝐿1/𝜁 with a universal scaling exponent 𝜁. Furthermore, we suggest an effective theory formulation describing the dynamics using one of the order parameters identified. The formation of a condensate at early times may have intriguing implications for the early stages in heavy-ion collisions.
J. Berges, K. Boguslavski, L. de Bruin, T. Butler, J. M. Pawlowski, „Order parameters for gauge invariant condensation far from equilibrium“, Phys. Rev. D 109, 114011 (2024).
https://journals.aps.org/prd/abstract/10.1103/PhysRevD.109.114011
Related to Project B03, A01
Abstract:
We calculate nonperturbative self-consistent fermionic and bosonic spectral functions of ultracold Fermi gases with the spectral functional approach. This approach allows for a direct real-time computation of nonperturbative correlation functions, and in the present work we use spectral Dyson-Schwinger equations. We focus on the normal phase of the spin-balanced Fermi gas and provide numerical results for the full fermionic and bosonic spectral functions. The spectral functions are then used for the determination of the equation of state, the Tan contact, and ejection rf spectra at unitarity. These results are compared to experimental data, the self-consistent 𝑇-matrix approach, and lattice results. Our approach offers a wide range of applications, including the ab initio calculation of transport and spectral properties of the superfluid phase in the BCS-BEC crossover.
E. Dizer, J. Horak, J. M. Pawlowski, „Spectral properties and observables in ultracold Fermi gases“, Phys. Rev. A 109, 063311 (2024).
https://journals.aps.org/pra/abstract/10.1103/PhysRevA.109.063311
Related to Project B03, C01
Abstract:
An impurity interacting with an ultracold Fermi gas can form either a polaron state or a dressed molecular state, the molaron, in which the impurity forms a bound state with one gas particle. This molaron state features rich physics, including a negative effective mass around unitarity and a first-order transition to the polaron state. However, these features have remained so far experimentally inaccessible. In this work we show theoretically how the molaron state can be directly prepared experimentally even in its excited states using Raman spectroscopy techniques. Initializing the system in the ultrastrong coupling limit, where the binding energy of the molaron is much larger than the Fermi energy, our protocol maps out the momentum-dependent spectral function of the molecule. Using a diagrammatic approach we furthermore show that the molecular spectral function serves as a direct precursor of the elusive Fulde-Ferell-Larkin-Ovchinnikov phase, which is realized for a finite density of fermionic impurity particles. Our results pave the way to a systematic understanding of how composite particles form in quantum many-body environments and provide a basis to develop new schemes for the observation of exotic phases of quantum many-body systems.
O. K. Diessel, J. von Milczewski, A. Christianen, R. Schmidt, „Probing molecular spectral
functions and unconventional pairing using Raman spectroscopy“, Phys. Rev. Res. 6, 023239
(2024).
https://journals.aps.org/prresearch/abstract/10.1103/PhysRevResearch.6.023239
Related to Project C01
Abstract:
We investigate a disorder-free quantum Ising chain subject to a time-periodic drive that rotates each spin by an angle 𝜋(1−𝜀𝑖). In case all spins experience the same deviation 𝜀 and the system is initialized in a fully polarized state, the dynamics is known to be time crystalline: the magnetization of the system exhibits period-doubled oscillations for timescales that grow exponentially with the length of the chain. In this work, we study the effect of a deviation 𝜀 that differs between spins. We find that reducing 𝜀 for a single spin drastically enhances the lifetime of spatiotemporal order, suggesting the name metronome spin. Employing perturbative arguments in an average Hamiltonian picture, we explain this observation for initial states with macroscopic bulk magnetization. Furthermore, in the case of random bit-string initial states, we report the enhancement of the lifetime of a topological edge mode, which can also be understood in the same picture. Finally, we discuss an altered geometry in which the metronome spin is not directly part of the chain, affecting the dynamics in different ways in the two scenarios considered. Our findings unveil the intricate dynamics that emerge in Floquet systems under the influence of a spatially varying drive, thereby uncovering new avenues for Floquet engineering.
N. Euler, A. Braemer, L. Benn, M. Gärttner, „Metronome spin stabilizes time-crystalline dynamics“,
Phys. Rev. B 109, 224301 (2024).
https://journals.aps.org/prb/abstract/10.1103/PhysRevB.109.224301
Related to Project A05
Abstract:
We implement two types of matter-wave interferometers using trapped Bose-condensed Feshbach molecules, from weak to strong interactions. In each case, we focus on investigating interaction effects and their implications for the performance. In the Ramsey-type interferometer where interference between the two motional quantum states in an optical lattice is observed, interparticle interactions are found to induce energy shifts in the states. Consequently, this results in a reduction of the interferometer frequency and introduces a phase shift during the lattice pulses used for state manipulation. Furthermore, nonuniformity leads to dephasing and collisional effects contribute to the degradation of contrast. In the Michelson-type interferometer, where matter waves are spatially split and recombined in a waveguide, interference is observed in the presence of significant interaction, however coherence degrades with increasing interaction strength. Notably, coherence is also observed in thermal clouds, indicating the white-light nature of the implemented Michelson-type interferometer.
C. Li, Q. Liang, P. Paranjape, R. Wu, J. Schmiedmayer, „Matter-wave interferometers with
trapped strongly interacting Feshbach molecules“, Phys. Rev. Res. 6, 023217 (2024).
https://journals.aps.org/prresearch/abstract/10.1103/PhysRevResearch.6.023217
Related to Project A03
Abstract:
A high-precision Penning-trap experiment was operated with a programmable 20 V Josephson voltage source, providing a significantly higher stability of the electrostatic trapping potential. This increased the motional frequency stability of a trapped ion by about a factor of two with respect to state-of-the-art voltage sources. An absolute axial frequency stability of 7.8(6) mHz corresponding to a relative precision of 9.7(8) x 10^-9 at 795 kHz was demonstrated using a trapped 9Be3+ ion as a measurement probe. The enhanced stability in the trapping potential opens up the possibility for improved determinations of the proton and antiproton magnetic moments and direct high-precision measurements of the nuclear magnetic moments of 2H, 3He, and 7Li. In the field of mass spectrometry, the developments will enable measurements of cyclotron frequency ratios and, thus, mass ratio measurements with unprecedented relative statistical uncertainties below the 10^-12 level.
A. Kaiser, S. Dickopf, M. Door, R. Behr, U. Beutel, S. Eliseev, A. Kaushik, K. Kromer, M.
Müller, L. Palafox, S. Ulmer, A. Mooser, K. Blaum, „Josephson voltage standards as ultrastable
low-noise voltage sources for precision Penning-trap experiments “, Appl. Phys. Lett.
124, 224002 (2024).
https://doi.org/10.1063/5.0206779
Related to Project B01
Abstract:
The production of virtual photons is a very sensitive probe of the properties of the quark-gluon plasma. As they are experimentally detected by lepton pairs, they suffer from a large background arising from hadron decays. Light-flavour hadrons dominate at low invariant masses below mee ~ 0.5 GeV and heavy flavours above. These contributions must therefore also be taken into account in experimental analyses at the LHC. In this paper, we calculate the direct contribution from virtual photons produced in the Drell-Yan process with an additional jet in POWHEG and find that it is significant at low invariant masses. We also simulate the background contributions from cc^\bar and bb^\bar production with POWHEG and quantify the theoretical uncertainties due to variations of the perturbative scales and parton distribution functions. We find larger relative and absolute uncertainties for the lighter c quarks than for heavier b quarks.
A. Andronic, T. Jezo, M. Klasen, C. Klein-Bösing, A. P. Neuwirth, „Di-electron production at
the LHC: unravelling virtual-photon and heavy-flavour contributions“, JHEP 05, 222 (2024).
https://link.springer.com/article/10.1007/JHEP05(2024)222
Related to Project C05
Abstract:
We compute the bound state properties of three-dimensional scalar 𝜙4 theory in the broken phase. To this end, we extend the recently developed technique of spectral Dyson-Schwinger equations to solve the Bethe-Salpeter equation and determine the bound state spectrum. We employ consistent truncations for the two-, three- and four-point functions of the theory that recover the scaling properties in the infinite coupling limit. Our result for the mass of the lowest-lying bound state in this limit agrees very well with lattice determinations.
G. Eichmann, A. Gómez, J. Horak, J. M. Pawlowski, J Wessely, N Wink, „Bound states from the spectral Bethe-Salpeter equation“, Phys. Rev. D 109, 096024 (2024).
https://journals.aps.org/prd/abstract/10.1103/PhysRevD.109.096024
Related to Project A02, B03, C01
Abstract:
We investigate pattern formation in two-dimensional Bose-Einstein condensates (BECs) caused by periodic driving of the interatomic interaction. We show that this modulation generically leads to a stable square grid density pattern, due to nonlinear effects beyond the initial Faraday instability. We take the amplitudes of two waves parametrizing the two-dimensional density pattern as order parameters in pattern formation. For these amplitudes, we derive a set of coupled time-evolution equations from the Gross-Pitaevskii equation with a time-periodic interaction. We identify the fixed points of the time evolution and show by stability analysis that the inhomogeneous density exhibits a square grid pattern, which can be understood as a manifestation of a stable fixed point. Our stability analysis establishes the pattern in BECs as a nonequilibrium steady state.
K. Fujii, S. L. Görlitz, N. Liebster, M. Sparn, E. Kath, H. Strobel, M. K. Oberthaler, T. Enss,
„Stable-fixed-point description of square-pattern formation in driven two-dimensional Bose-
Einstein condensates“, Phys. Rev. A 109, L051301 (2024).
https://journals.aps.org/pra/abstract/10.1103/PhysRevA.109.L051301
Related to Project C02, C03, A04
Abstract:
In the hydrodynamics of integrable models, diffusion is a subleading correction to ballistic propagation. Here we quantify the diffusive contribution for one-dimensional Bose gases and find it most influential in the crossover between the main thermodynamic regimes of the gas. Analysing the experimentally measured dynamics of a single density mode, we find diffusion to be relevant only for high wavelength excitations. Instead, the observed relaxation is solely caused by a ballistically driven dephasing process, whose time scale is related to the phonon lifetime of the system and is thus useful to evaluate the applicability of the phonon bases typically used in quantum field simulators.
F. Møller, F. Cataldini, J. Schmiedmayer, „Identifying diffusive length scales in one-dimensional
Bose gases“, SciPost Phys. Core 7, 025 (2024).
https://scipost.org/10.21468/SciPostPhysCore.7.2.025
Related to Project A03
Abstract:
We present a review of the conceptual basis, current knowledge, and recent progress regarding global analysis of nuclear parton distribution functions (PDFs). After introducing the theoretical foundations and methodological approaches for the extraction of nuclear PDFs from experimental data, we discuss how different measurements in fixed-target and collider experiments provide increasingly precise constraints on various aspects of nuclear PDFs, including shadowing, antishadowing, the EMC effect, Fermi motion, flavor separation, deuteron binding, and target-mass and other higher-twist effects. Particular emphasis is given to measurements carried out in proton–lead collisions at the Large Hadron Collider, which have revolutionized the global analysis during the past decade. These measurements include electroweak boson, jet, light hadron, and heavy flavor observables. Finally, we outline the expected impact of the future Electron Ion Collider and discuss the role and interplay of nuclear PDFs with other branches of nuclear, particle, and astroparticle physics.
M. Klasen, H. Paukkunen, „ Nuclear Parton Distribution Functions After the First Decade of LHC Data “, Annu. Rev. Nucl. Part. Sci. 74, 49 (2024).
https://www.annualreviews.org/content/journals/10.1146/annurev-nucl-102122-022747
Related to Project C05
Abstract:
We present an optical aberration correction technique for ultracold quantum gas experiments which directly utilizes the quantum gas as a wavefront sensor. The direct use of the quantum gas enables correcting aberrations that are otherwise impractical to measure, e.g. introduced by vacuum windows. We report a root-mean-square precision and accuracy of 0.01{\lambda} and 0.03{\lambda}, respectively, and also show independently the reduction of aberrations through measurement of the trap frequency of our optical tweezer. These improvements were achieved for a tweezer size that is well below our imaging resolution. The present work is in particular intended to serve as a tutorial for experimentalists interested in implementing similar methods in their experiment.
P. Hill, P. Lunt, J. Reiter, M. Galka, P. Preiss, S. Jochim, „Optical Phase Aberration Correction with an Ultracold Quantum Gas“, 25. Apr. 2024, arXiv:2404.16827 (2024).
https://arxiv.org/abs/2404.16827
Related to Project C01, C02
Abstract:
The investigation of the absolute scale of the effective neutrino mass remains challenging due to the exclusively weak interaction of neutrinos with all known particles in the standard model of particle physics. At present, the most precise and least-model-dependent upper limit on the electron antineutrino mass is set by the Karlsruhe Tritium Neutrino Experiment (KATRIN) from the analysis of the tritium β-decay. Another promising approach is the electron capture in 163Ho, which is under investigation using microcalorimetry by the Electron Capture in Holmium (ECHo) and HOLMES collaborations. An independently measured Q value for this process is vital for the assessment of systematic uncertainties in the neutrino mass determination. Here we report a direct, independent determination of this Q value by measuring the free-space cyclotron frequency ratio of highly charged ions of 163Ho and 163Dy in the Penning-trap experiment PENTATRAP. Combining this ratio with atomic physics calculations of the electronic binding energies yields a Q value of 2,863.2 ± 0.6 eV c−2, which represents a more than 50-fold improvement over the state of the art. This will enable the determination of the electron neutrino mass on a sub-electronvolt level from the analysis of the electron capture in 163Ho.
M. W. Haverkort, C. H. Keitel, K. Blaum et al., „Penning-trap measurement of the Q value of
electron capture in 163Ho for the determination of the electron neutrino mass“, Nature Phys.
20, 921 (2024).
https://www.nature.com/articles/s41567-024-02461-9
Related to Project B01, B02
Abstract:
The scaling of local quantum entropies is of utmost interest for characterizing quantum fields, many-body systems, and gravity. Despite their importance, theoretically and experimentally accessing quantum entropies is challenging as they are nonlinear functionals of the underlying quantum state. Here, we show that suitably chosen classical entropies capture the very same features as their quantum analogs for an experimentally relevant setting. We describe the post-quench dynamics of a multi-well spin-1 Bose-Einstein condensate from an initial product state via measurement distributions of spin observables and estimate the corresponding entropies using the asymptotically unbiased k-nearest neighbor method. We observe the dynamical build-up of quantum correlations signaled by an area law, as well as local thermalization revealed by a transition to a volume law, both in regimes characterized by non-Gaussian distributions. We emphasize that all relevant features can be observed at small sample numbers without assuming a specific functional form of the distributions, rendering our method directly applicable to a large variety of models and experimental platforms.
Y. Deller, M. Gärttner, T. Haas, M. K. Oberthaler, M. Reh, H. Strobel, „Area laws and thermalization
from classical entropies in a Bose-Einstein condensate“, 18. Apr. 2024, arXiv:2404.
12321 (2024).
https://arxiv.org/abs/2404.12321
Related to Project A06
Abstract:
Many homogeneous, four-dimensional space-time geometries can be considered within real projective geometry, which yields a mathematically well-defined framework for their deformations and limits without the appearance of singularities. Focussing on generalized unitary transformation behavior, projective quantum fields can be axiomatically introduced, which transform smoothly under geometry deformations and limits. Connections on the related projective frame bundles provide gauge fields with gauge group PGL5R. For Poincaré geometry, on operator level only P(GL2R×GL3R)≅R≠0×PGL2R×PGL3R gauge bosons can interact non-trivially with other projective quantum fields from the non- to ultra-relativistic limits. The corresponding propagating, complexified gauge bosons come with the Standard Model gauge group GSM=(U(1)×SU(2)×SU(3))/Z6. Physical scale transformations can act as global gauge transformations and their spontaneous breaking can lead to masses for the projective quantum fields including the SU(2) gauge bosons. Projective quantum fields, which are irreducible both with respect to the Lie algebra pgl5R and the Poincaré group, form Dirac fermions and GSM gauge bosons interact with them similar to the Standard Model. For homogeneous, curved Lorentz geometries a gauge group similar to the gauge group of metric-affine gravity appears.
D. Spitz, „Similarities between projective quantum fields and the Standard Model“, 17. Apr.
2024, arXiv:2404.11425 (2024).
https://arxiv.org/abs/2404.11425
Related to Project
Abstract:
The formation of dispersive shock waves in one-dimensional Bose gas represents a limitation of Generalized Hydrodynamics (GHD) due to the coarse-grained nature of the theory. Nevertheless, GHD accurately captures long-wavelength behavior, thus indicating an implicit knowledge of the underlying microscopic physics. Such representations are already known through the Whitham modulation theory, where dispersionless equations describe the evolution of the slowly varying shock wave parameters. Here we study the correspondence between Whitham’s approach to the Gross-Pitaevskii equation and GHD in the semiclassical limit and beyond. Our findings enable the recovery of the shock wave solution directly from GHD simulations, which we demonstrate for both zero and finite temperature. Additionally, we study how free expansion protocols affect the shock wave density and their implications for experimental detection. The combined picture of Whitham and GHD lends itself to additional physical interpretation regarding the formation of shock waves.
F. Møller, P. Schüttelkopf, J. Schmiedmayer, S. Erne, „Whitham approach to Generalized
Hydrodynamics“, Phys. Rev. Res. 6, 013328 (2024).
https://journals.aps.org/prresearch/abstract/10.1103/PhysRevResearch.6.013328
Related to Project A03
Abstract:
Considering homogeneous four-dimensional space-time geometries within real projective geometry provides a mathematically well-defined framework to discuss their deformations and limits without the appearance of coordinate singularities. On Lie algebra level the related conjugacy limits act isomorphically to concatenations of contractions. We axiomatically introduce projective quantum fields on homogeneous space-time geometries, based on correspondingly generalized unitary transformation behavior and projectivization of the field operators. Projective correlators and their expectation values remain well-defined in all geometry limits, which includes their ultraviolet and infrared limits. They can degenerate with support on space-time boundaries and other lower-dimensional space-time subspaces. We explore fermionic and bosonic superselection sectors as well as the irreducibility of projective quantum fields. Dirac fermions appear, which obey spin-statistics as composite quantum fields. The framework might be of use for the consistent description of quantum fields in holographic correspondences and their flat limits.
D. Spitz, „Quantum fields on projective geometries“, 26. März 2024, arXiv:2403.17996 (2024).
https://arxiv.org/abs/2403.17996
Related to Project
Abstract:
Quantum simulators built from ultracold atoms promise to study quantum phenomena in interacting many-body systems. However, it remains a challenge to experimentally prepare strongly correlated continuous systems such that the properties are dominated by quantum fluctuations. Here, we show how to enhance the quantum correlations in a one-dimensional multimode bosonic Josephson junction, which is a quantum simulator of the sine-Gordon field theory. Our approach is based on the ability to track the nonequilibrium dynamics of quantum properties. After creating a bosonic Josephson junction at the stable fixed point of the classical phase space, we observe squeezing oscillations in the two conjugate variables. We show that the squeezing oscillation frequency can be tuned by more than one order of magnitude, and we are able to achieve a spin squeezing close to 10 dB by utilizing these oscillatory dynamics. The impact of improved spin squeezing is directly revealed by detecting enhanced spatial phase correlations between decoupled condensates. Our work provides new ways for engineering correlations and entanglement in the external degree of freedom of interacting many-body systems.
T. Zhang, M. Maiwöger, F. Borselli, Y. Kuriatnikov, J. Schmiedmayer, M. Prüfer, „Squeezing Oscillations in a Multimode Bosonic Josephson Junction“, Phys. Rev. X 14, 011049 (2024).
https://journals.aps.org/prx/abstract/10.1103/PhysRevX.14.011049
Related to Project A03
Abstract:
We study nonequilibrium dynamics of relativistic 𝑁-component scalar field theories in Minkowski space-time in a classical statistical regime, where typical occupation numbers of modes are much larger than unity. In this strongly correlated system far from equilibrium, the role of different phenomena such as nonlinear wave propagation and defect dynamics remains to be clarified. We employ persistent homology to infer topological features of the nonequilibrium many-body system for different numbers of field components 𝑁 via a hierarchy of cubical complexes. Specifically, we show that the persistent homology of local energy density fluctuations can give rise to signatures of self-similar scaling associated with topological defects, distinct from the scaling behavior of nonlinear wave modes. This contributes to the systematic understanding of the role of topological defects for far-from-equilibrium time evolutions of nonlinear many-body systems.
V. Noel, D. Spitz, „Detecting defect dynamics in relativistic field theories far from equilibrium
using topological data analysis“, Phys. Rev. D 109, 056011 (2024).
https://journals.aps.org/prd/abstract/10.1103/PhysRevD.109.056011
Related to Project A04, B03
Abstract:
We use QCD kinetic theory to compute photon production in the chemically equilibrating Quark-Gluon Plasma created in the early stages of high-energy heavy-ion collisions. We do a detailed comparison of pre-equilibrium photon rates to the thermal photon production. We show that the photon spectrum radiated from a hydrodynamic attractor evolution satisfies a simple scaling form in terms of the specific shear viscosity η/s and entropy density dS/dζ ∼ (Tτ1/3)3/2∞. We confirm the analytical predictions with numerical kinetic theory simulations. We use the extracted scaling function to compute the pre-equilibrium photon contribution in = 2.76 TeV 0–20% PbPb collisions. We demonstrate that our matching procedure allows for a smooth switching from pre-equilibrium kinetic to thermal hydrodynamic photon production. Finally, our publicly available implementation can be straightforwardly added to existing heavy ion models.
O. Garcia-Montero, A. Mazeliauskas, P. Plaschke, S. Schlichting, „Pre-equilibrium photons
from the early stages of heavy-ion collisions“, JHEP 2024, 053 (2024).
https://link.springer.com/article/10.1007/JHEP03(2024)053
Related to Project A01
Abstract:
Vacuum birefringence produces a differential phase between orthogonally polarized components of a weak electromagnetic probe in the presence of a strong electromagnetic field. Despite representing a hallmark prediction of quantum electrodynamics, vacuum birefringence remains untested in pure light configurations due to the extremely large electromagnetic fields required for a detectable phase difference. Here, we exploit the programmable focal velocity and extended focal range of a flying focus laser pulse to substantially lower the laser power required for detection of vacuum birefringence. In the proposed scheme, a linearly polarized x-ray probe pulse counterpropagates with respect to a flying focus pulse, whose focus moves at the speed of light in the same direction as the x-ray probe. The peak intensity of the flying focus pulse overlaps the probe over millimeter-scale distances and induces a polarization ellipticity on the order of 10−10, which lies within the detection sensitivity of existing x-ray polarimeters.
M. Formanek, J. P. Palastro, D. Ramsey, S. Weber, A. Di Piazza, „Signatures of vacuum birefringence
in low-power flying focus pulses“, Phys. Rev. D 109, 056009 (2024).
https://journals.aps.org/prd/abstract/10.1103/PhysRevD.109.056009
Related to Project B02
Abstract:
Important properties of complex quantum many-body systems and their phase diagrams can often already be inferred from the impurity limit. The Bose polaron problem describing an impurity atom immersed in a Bose-Einstein condensate is a paradigmatic example. The interplay between the impurity-mediated attraction between the bosons and their intrinsic repulsion makes this model rich and interesting, but also complex to describe theoretically. To tackle this challenge, we develop a quantum chemistry-inspired computational technique and compare two variational methods that fully include both the boson-impurity and interboson interactions. We find one regime where the impurity-mediated interactions overcome the repulsion between the bosons, so that a sweep of the boson-impurity interaction strength leads to an instability of the polaron due to the formation of many-body clusters. If instead the interboson interactions dominate, the impurity will experience a crossover from a polaron into a few-body bound state. We achieve a unified understanding incorporating both of these regimes and show that they are experimentally accessible. Moreover, we develop an analytical model that allows us to interpret these phenomena in the Landau framework of phase transitions, revealing a deep connection of the Bose polaron model to both few- and many-body physics.
A. Christianen, J. I. Cirac, R. Schmidt, „Phase diagram for strong-coupling Bose polarons“,
SciPost Phys. 16, 067 (2024).
https://scipost.org/SciPostPhys.16.3.067
Related to Project C07
Abstract:
A remarkable double-copy relation of Einstein gravity to QCD in Regge asymptotics is Γ𝜇𝜈=1/2𝐶𝜇𝐶𝜈−1/2𝑁𝜇𝑁𝜈, where Γ𝜇𝜈 is the gravitational Lipatov vertex in the 2→3 graviton scattering amplitude, 𝐶𝜇 its Yang-Mills counterpart, and 𝑁𝜇 the QED bremsstrahlung vertex. In QCD, the Lipatov vertex is a fundamental building block of the BFKL equation describing the 2→𝑁 scattering of gluons at high energies. Likewise, the gravitational Lipatov vertex is a key ingredient in a 2D effective field theory framework describing trans-Planckian 2→𝑁 graviton scattering. We construct a quantitative correspondence between a semiclassical Yang-Mills framework for radiation in gluon shockwave collisions and its counterpart in general relativity. In particular, we demonstrate the Lipatov double copy in a dilute-dilute approximation corresponding to 𝑅𝑆,𝐿, 𝑅𝑆,𝐻≪𝑏, where 𝑅𝑆,𝐿, 𝑅𝑆,𝐻 are the respective emergent Schwarzchild radii generated in shockwave collisions and 𝑏 is the impact parameter. We outline extensions of the correspondence developed here to the dilute-dense computation of gravitational wave radiation in the close vicinity of one of the black holes, the construction of graviton propagators in the shockwave background, and a renormalization group approach to compute 2→𝑁 amplitudes that incorporates graviton Reggeization and coherent graviton multiple scattering.
H. Raj, R. Venugopalan, „Universal features of 2 → N scattering in QCD and gravity from shockwave collisions“, Phys. Rev. D 109, 044064 (2024).
https://journals.aps.org/prd/abstract/10.1103/PhysRevD.109.044064
Related to Project C05, Co6
Abstract:
The strongly attractive Fermi gas in the BCS-BEC crossover is efficiently described in terms of coupled fermions and fermion pairs, or molecules. We compute the spectral functions of both fermions and pairs in the normal state near the superfluid transition using a Keldysh formulation in real frequency. The mutual influence between fermions and pairs is captured by solving the self-consistent Luttinger-Ward equations: These include both the damping of fermions by scattering off dressed pairs and the decay of pair states by dissociation into two dressed fermions. The pair spectra encode contact correlations between fermions and form the basis for computing dynamical response functions and transport properties.
T. Enss, „Particle and pair spectra for strongly correlated Fermi gases: A real-frequency solver“,
Phys. Rev. A 109, 023325 (2024).
https://journals.aps.org/pra/abstract/10.1103/PhysRevA.109.023325
Related to Project C03, C02, ABC
Abstract:
We study how isotropic and homogeneous far-from-equilibrium quantum systems relax to nonthermal attractors, which are of interest for cold atoms and nuclear collisions. We demonstrate that a first-order ordinary differential equation governs the self-similar approach to nonthermal attractors, i.e., the prescaling. We also show that certain natural scaling-breaking terms induce logarithmically slow corrections that prevent the scaling exponents from reaching the constant values during the system’s lifetime. We propose that, analogously to hydrodynamic attractors, the appropriate mathematical structure to describe such dynamics is the transseries. We verify our analytic predictions with state-of-the-art 2PI simulations of the large-𝑁 vector model and QCD kinetic theory.
M. P. Heller, A. Mazeliauskas, T. Preis, „Prescaling Relaxation to Nonthermal Attractors“,
Phys. Rev. Lett. 132, 071602 (2024).
https://journals.aps.org/prl/abstract/10.1103/PhysRevLett.132.071602
Related to Project A01
Abstract:
Whether or not femto-scale droplets of quark-gluon plasma (QGP) are formed in so-called small systems at high-energy colliders is a pressing question in the phenomenology of the strong interaction. For proton-proton or proton-nucleus collisions the answer is inconclusive due to the large theoretical uncertainties plaguing the description of these processes. While upcoming data on collisions of 16O nuclei may mitigate these uncertainties in the near future, here we demonstrate the unique possibilities offered by complementing 16O16O data with collisions of 20Ne ions. We couple both NLEFT and PGCM ab initio descriptions of the structure of 20Ne and 16O to hydrodynamic simulations of 16O16O and 20Ne20Ne collisions at high energy. We isolate the imprints of the bowling-pin shape of 20Ne on the collective flow of hadrons, which can be used to perform quantitative tests of the hydrodynamic QGP paradigm. In particular, we predict that the elliptic flow of 20Ne20Ne collisions is enhanced by as much as 1.170(8)stat.(30)syst. for NLEFT and 1.139(6)stat.(39)syst. for PGCM relative to 16O16O collisions for the 1% most central events. At the same time, theoretical uncertainties largely cancel when studying relative variations of observables between two systems. This demonstrates a method based on experiments with two light-ion species for precision characterizations of the collective dynamics and its emergence in a small system.
G. Giacalone et al., „The unexpected uses of a bowling pin: exploiting 20Ne isotopes for precision
characterizations of collectivity in small systems“, 8. Feb. 2024, arXiv:2402.05995 (2024).
https://arxiv.org/abs/2402.05995
Related to Project
Abstract:
Physical systems can be used as an information processing substrate and, with that, extend traditional computing architectures. For such an application, the experimental platform must guarantee pristine control of the initial state, the temporal evolution, and readout. All these ingredients are provided by modern experimental realizations of atomic Bose-Einstein condensates. By embedding a quantum gas experiment in a machine learning pipeline, one can represent nonlinear functions while only linear operations on classical computers of the pipeline are necessary. We demonstrate successful regression and interpolation of a nonlinear function using an elongated cloud of potassium atoms and characterize the performance of our system.
M. Hans, E. Kath, M. Sparn, N. Liebster, F. Draxler, C. Schnörr, H. Strobel, M. K. Oberthaler,
„Bose-Einstein condensate experiment as a nonlinear block of a machine learning pipeline“, Phys. Rev. Res. 6, 013122 (2024).
https://journals.aps.org/prresearch/abstract/10.1103/PhysRevResearch.6.013122
Related to Project A04
Abstract:
In recent years, Rydberg excitations in atomic quantum gases have become a successful platform to explore quantum impurity problems. A single impurity immersed in a Fermi gas leads to the formation of a polaron, a quasiparticle consisting of the impurity being dressed by the surrounding medium. With a radius of about the Fermi wavelength, the density profile of a polaron cannot be explored using in situ optical imaging techniques. In this Letter, we propose a new experimental measurement technique that enables the in situ imaging of the polaron cloud in ultracold quantum gases. The impurity atom induces the formation of a polaron cloud and is then excited to a Rydberg state. Because of the mesoscopic interaction range of Rydberg excitations, which can be tuned by the principal numbers of the Rydberg state, atoms extracted from the polaron cloud form dimers with the impurity. By performing first principle calculations of the absorption spectrum based on a functional determinant approach, we show how the occupation of the dimer state can be directly observed in spectroscopy experiments and can be mapped onto the density profile of the gas particles, hence providing a direct, real-time, and in situ measure of the polaron cloud.
M. Gievers, M.Wagner, R. Schmidt, „Probing Polaron Clouds by Rydberg Atom Spectroscopy“,
Phys. Rev. Lett. 132, 053401 (2024).
https://journals.aps.org/prl/abstract/10.1103/PhysRevLett.132.053401
Related to Project C01, C07
Abstract:
We explore a supervised machine-learning approach to estimate the entanglement entropy of multiqubit systems from few experimental samples. We put a particular focus on estimating both aleatoric and epistemic uncertainty of the network’s estimate and benchmark against the best-known conventional estimation algorithms. For states that are contained in the training distribution, we observe convergence in a regime of sample sizes in which the baseline method fails to give correct estimates, while extrapolation only seems possible for regions close to the training regime. As a further application of our method, highly relevant for quantum simulation experiments, we estimate the quantum mutual information for nonunitary evolution by training our model on different noise strengths.
M. Rieger, M. Reh, M. Gärttner, „Sample-efficient estimation of entanglement entropy through supervised learning“, Phys. Rev. A 109, 012403 (2024).
https://journals.aps.org/pra/abstract/10.1103/PhysRevA.109.012403
Related to Project A06
Abstract:
We investigate false vacuum decay of a relativistic scalar field initialized in the metastable minimum of an asymmetric double-well potential. The transition to the true ground state is a well-defined initial-value problem in real time, which can be formulated in nonequilibrium quantum field theory on a closed time path. We employ the nonperturbative framework of the two-particle irreducible (2PI) quantum effective action at next-to-leading order in a large-𝑁 expansion. We also compare to classical-statistical field theory simulations on a lattice in the high-temperature regime. By this, we demonstrate that the real-time decay rates are comparable to those obtained from the conventional Euclidean (bounce) approach. In general, we find that the decay rates are time dependent. For a more comprehensive description of the dynamics, we extract a time-dependent effective potential, which becomes convex during the nonequilibrium transition process. By solving the quantum evolution equations for the one- and two-point correlation functions for vacuum initial conditions, we demonstrate that quantum corrections can lead to transitions that are not captured by classical-statistical approximations.
L. Batini, A. Chatrchyan, J. Berges, „Real-time dynamics of false vacuum decay“, Phys. Rev. D 109, 023502 (2024).
https://journals.aps.org/prd/abstract/10.1103/PhysRevD.109.023502
Related to Project B04
Abstract:
A phenomenological analysis of the experimental measurements of transverse momentum spectra of identified charged hadrons and strange hyperons in Pb-Pb and Xe-Xe collisions at the CERN Large Hadron Collider (LHC) is presented. The analysis is based on the relativistic fluid dynamics description implemented in the numerically efficient Fluid𝑢M approach. Building on our previous work, we separate in our treatment the chemical and kinetic freeze-outs, and incorporate the partial chemical equilibrium to describe the late stages of the collision evolution. This analysis makes use of Bayesian inference to determine key parameters of the quark-gluon plasma (QGP) evolution and its properties including the shear and bulk viscosity to entropy ratios, the initialization time, the initial entropy density, and the freeze-out temperatures. The physics parameters and their posterior probabilities are extracted using a global search in multidimensional space with modern machine learning tools, such as ensembles of neural networks. We employ our newly developed fast framework to assess systematic uncertainties in the extracted model parameters by systematically varying key components of our analysis.
L. Vermunt, Y. Seemann, A. Dubla, S. Floerchinger, E. Grossi, A. Kirchner, S. Masciocchi, I.
Selyuzhenkov, „Mapping properties of the quark gluon plasma in Pb-Pb and Xe-Xe collisions
at energies available at the CERN Large Hadron Collider“, Phys. Rev. C 108, 064908 (2023).
https://journals.aps.org/prc/abstract/10.1103/PhysRevC.108.064908
Related to Project C06
Abstract:
We present the measurements of individual bound electron g factors of 20Ne9+ and 22Ne9+ on the relative level of 0.1 parts per billion. The comparison with theory represents the most stringent test of bound-state QED in strong electric fields. A dedicated mass measurement results in m(20Ne)=19.992 440 168 77(9) u, which improves the current literature value by a factor of 18, disagrees by 4 standard deviations, and represents the most precisely measured mass value in atomic mass units. Together, these measurements yield an electron mass on the relative level of 0.1 ppb with me=5.485 799 090 99(59)×10−4 u as well as a factor of seven improved m(22Ne)=21.991 385 098 2(26) u.
F. Heiße, M. Door, T. Sailer, P. Filianin, J. Herkenhoff, C. M. König, K. Kromer, D. Lange,
J. Morgner, A. Rischka, Ch. Schweiger, B. Tu, Y. N. Novikov, S. Eliseev, S. Sturm, K. Blaum, „High-Precision Determination of g Factors and Masses of 20Ne9+ and 22Ne9+“, Phys. Rev.Lett. 131, 253002 (2023).
https://journals.aps.org/prl/abstract/10.1103/PhysRevLett.131.253002
Related to Project B01
Abstract:
A fluid-dynamic approach to charm-quark diffusion in the quark-gluon plasma (QGP) is developed for the first time. Results for integrated yields and momentum distributions of charmed hadrons obtained with a fluid-dynamic description for the dynamics of the QGP coupled to an additional heavy-quark-antiquark current are shown. In addition to the thermodynamic equation of state, this description uses a heavy-quark diffusion constant which we take from lattice QCD calculations. The results describe the experimental data measured at the LHC at the center-of-mass energy of √𝑠NN=5.02 TeV up to 𝑝T∼4–5 GeV/𝑐, showing that charm quarks undergo a very fast hydrodynamization in the medium created by ultrarelativistic heavy-ion collisions.
F. Capellino, A. Dubla, S. Floerchinger, E. Grossi, A. Kirchner, S. Masciocchi, „Fluid dynamics
of charm quarks in the quark-gluon plasma“, Phys. Rev. D 108, 116011 (2023).
https://journals.aps.org/prd/abstract/10.1103/PhysRevD.108.116011
Related to Project A02
Abstract:
In nucleus–nucleus collisions at ultra-relativistic energies, a new kind of matter is created: the Quark–Gluon Plasma. Peter Braun-Munzinger, Anar Rustamov, and Johanna Stachel report on the phase diagram of hadronic matter at high temperature and low net baryon density. A connection is made between the experimentally determined chemical freeze-out points and the pseudo-critical temperature for the chiral crossover transition computed in lattice QCD. The role of fluctuations giving experimental access to the nature of the chiral phase transition will be summarized. Azimuthal anisotropies of hadron distributions show that the Quark–Gluon Plasma formed in high-energy collisions is strongly coupled, allowing us to deduce bulk and shear viscosities. In the hot and dense plasma, partons lose a large fraction of their energy, and this observation leads to the determination of another medium parameter: a jet transport coefficient. Quarkonia and their role as a probe of deconfinement form the final topic of their contribution.
The phase structure of strongly interacting matter at low temperature and high density is discussed by Kenji Fukushima. In this region of the phase diagram that is probed, for example, in neutron stars, different phases and phase transitions are expected on theoretical grounds. Astrophysical observations and the observation of gravitational waves lead to important constraints for calculations modeling the transitions into a quarkyonic regime, into quark matter, or color-superconducting states. The theoretical challenges to locate a conjectured critical end point in the QCD phase diagram are discussed.
P. Braun-Munzinger, A. Rustamov, J. Stachel, „QCD under extreme conditions“, Eur.Phys.J.C
83, 1125 (2023).
https://link.springer.com/article/10.1140/epjc/s10052-023-11949-2
Related to Project A01, A02, C05, C06
Abstract:
Quantum Chromodynamics, the theory of quarks and gluons, whose interactions can be described by a local SU(3) gauge symmetry with charges called “color quantum numbers”, is reviewed; the goal of this review is to provide advanced Ph.D. students a comprehensive handbook, helpful for their research. When QCD was “discovered” 50 years ago, the idea that quarks could exist, but not be observed, left most physicists unconvinced. Then, with the discovery of charmonium in 1974 and the explanation of its excited states using the Cornell potential, consisting of the sum of a Coulomb-like attraction and a long range linear confining potential, the theory was suddenly widely accepted. This paradigm shift is now referred to as the November revolution. It had been anticipated by the observation of scaling in deep inelastic scattering, and was followed by the discovery of gluons in three-jet events. The parameters of QCD include the running coupling constant, , that varies with the energy scale characterising the interaction, and six quark masses. QCD cannot be solved analytically, at least not yet, and the large value of at low momentum transfers limits perturbative calculations to the high-energy region where (250 MeV). Lattice QCD (LQCD), numerical calculations on a discretized space-time lattice, is discussed in detail, the dynamics of the QCD vacuum is visualized, and the expected spectra of mesons and baryons are displayed. Progress in lattice calculations of the structure of nucleons and of quantities related to the phase diagram of dense and hot (or cold) hadronic matter are reviewed. Methods and examples of how to calculate hadronic corrections to weak matrix elements on a lattice are outlined. The wide variety of analytical approximations currently in use, and the accuracy of these approximations, are reviewed. These methods range from the Bethe–Salpeter, Dyson–Schwinger coupled relativistic equations, which are formulated in both Minkowski or Euclidean spaces, to expansions of multi-quark states in a set of basis functions using light-front coordinates, to the AdS/QCD method that imbeds 4-dimensional QCD in a 5-dimensional deSitter space, allowing confinement and spontaneous chiral symmetry breaking to be described in a novel way. Models that assume the number of colors is very large, i.e. make use of the large -limit, give unique insights. Many other techniques that are tailored to specific problems, such as perturbative expansions for high energy scattering or approximate calculations using the operator product expansion are discussed. The very powerful effective field theory techniques that are successful for low energy nuclear systems (chiral effective theory), or for non-relativistic systems involving heavy quarks, or the treatment of gluon exchanges between energetic, collinear partons encountered in jets, are discussed. The spectroscopy of mesons and baryons has played an important historical role in the development of QCD. The famous X,Y,Z states – and the discovery of pentaquarks – have revolutionized hadron spectroscopy; their status and interpretation are reviewed as well as recent progress in the identification of glueballs and hybrids in light-meson spectroscopy. These exotic states add to the spectrum of expected mesons and qqq baryons. The progress in understanding excitations of light and heavy baryons is discussed. The nucleon as the lightest baryon is discussed extensively, its form factors, its partonic structure and the status of the attempt to determine a three-dimensional picture of the parton distribution. An experimental program to study the phase diagram of QCD at high temperature and density started with fixed target experiments in various laboratories in the second half of the 1980s, and then, in this century, with colliders. QCD thermodynamics at high temperature became accessible to LQCD, and numerical results on chiral and deconfinement transitions and properties of the deconfined and chirally restored form of strongly interacting matter, called the Quark–Gluon Plasma (QGP), have become very precise by now. These results can now be confronted with experimental data that are sensitive to the nature of the phase transition. There is clear evidence that the QGP phase is created. This phase of QCD matter can already be characterized by some properties that indicate, within a temperature range of a few times the pseudocritical temperature, the medium behaves like a near ideal liquid. Experimental observables are presented that demonstrate deconfinement. High and ultrahigh density QCD matter at moderate and low temperatures shows interesting features and new phases that are of astrophysical relevance. They are reviewed here and some of the astrophysical implications are discussed. Perturbative QCD and methods to describe the different aspects of scattering processes are discussed. The primary parton–parton scattering in a collision is calculated in perturbative QCD with increasing complexity. The radiation of soft gluons can spoil the perturbative convergence, this can be cured by resummation techniques, which are also described here. Realistic descriptions of QCD scattering events need to model the cascade of quark and gluon splittings until hadron formation sets in, which is done by parton showers. The full event simulation can be performed with Monte Carlo event generators, which simulate the full chain from the hard interaction to the hadronic final states, including the modelling of non-perturbative components. The contribution of the LEP experiments (and of earlier collider experiments) to the study of jets is reviewed. Correlations between jets and the shape of jets had allowed the collaborations to determine the “color factors” – invariants of the SU(3) color group governing the strength of quark–gluon and gluon–gluon interactions. The calculated jet production rates (using perturbative QCD) are shown to agree precisely with data, for jet energies spanning more than five orders of magnitude. The production of jets recoiling against a vector boson, or Z, is shown to be well understood. The discovery of the Higgs boson was certainly an important milestone in the development of high-energy physics. The couplings of the Higgs boson to massive vector bosons and fermions that have been measured so far support its interpretation as mass-generating boson as predicted by the Standard Model. The study of the Higgs boson recoiling against hadronic jets (without or with heavy flavors) or against vector bosons is also highlighted. Apart from the description of hard interactions taking place at high energies, the understanding of “soft QCD” is also very important. In this respect, Pomeron – and Odderon – exchange, soft and hard diffraction are discussed. Weak decays of quarks and leptons, the quark mixing matrix and the anomalous magnetic moment of the muon are processes which are governed by weak interactions. However, corrections by strong interactions are important, and these are reviewed. As the measured values are incompatible with (most of) the predictions, the question arises: are these discrepancies first hints for New Physics beyond the Standard Model? This volume concludes with a description of future facilities or important upgrades of existing facilities which improve their luminosity by orders of magnitude. The best is yet to come!
P. Braun-Munzinger, A. Rustamov, J. Stachel et al., „50 Years of quantum chromodynamics“, Eur. Phys. J. C 83, 1125 (2023).
https://link.springer.com/article/10.1140/epjc/s10052-023-11949-2
Related to Project A01, A02, C05, C06
Abstract:
Quantum entanglement has been identified as a crucial concept underlying many intriguing phenomena in condensed matter systems, such as topological phases or many-body localization. Recently, instead of considering mere quantifiers of entanglement such as entanglement entropy, the study of entanglement structure in terms of the entanglement spectrum has shifted to a focus leading to new insights into fractional quantum Hall states and topological insulators, among others. What remains a challenge is the experimental detection of such fine-grained properties of quantum systems. The development of protocols for detecting features of the entanglement spectrum in cold-atom systems, which are one of the leading platforms for quantum simulation, is thus highly desirable and will open up new avenues for experimentally exploring quantum many-body physics. Here, we present a method to bound the width of the entanglement spectrum, or entanglement dimension, of cold atoms in lattice geometries, requiring only measurements in two experimentally accessible bases and utilizing ballistic time-of-flight (TOF) expansion. Building on previous proposals for entanglement certification for photon pairs, we first consider entanglement between two atoms of different atomic species and later generalize to higher numbers of atoms per species and multispecies configurations showing multipartite high-dimensional entanglement. Through numerical simulations, we show that our method is robust against typical experimental noise effects and thus will enable high-dimensional entanglement certification in systems of up to eight atoms using currently available experimental techniques.
N. Euler, M. Gärttner, „Detecting High-Dimensional Entanglement in Cold-Atom Quantum Simulators“, PRX Quantum 4, 040338 (2023).
https://journals.aps.org/prxquantum/abstract/10.1103/PRXQuantum.4.040338
Related to Project A06
Abstract:
Highly charged ions (HCIs) offer many opportunities for next-generation clock research due to the vast landscape of available electronic transitions in different charge states. The development of extreme ultraviolet frequency combs has enabled the search for clock transitions based on shorter wavelengths in HCIs. However, without initial knowledge of the energy of the clock states, these narrow transitions are difficult to be probed by lasers. In this Letter, we provide experimental observation and theoretical calculation of a long-lived electronic state in Nb-like Pb41+ that could be used as a clock state. With the mass spectrometer PENTATRAP, the excitation energy of this metastable state is directly determined as a mass difference at an energy of 31.2(8) eV, corresponding to one of the most precise relative mass determinations to date with a fractional uncertainty of 4×10−12. This experimental result agrees within 1σ with two partially different ab initio multiconfiguration Dirac-Hartree-Fock calculations of 31.68(13) eV and 31.76(35) eV, respectively. With a calculated lifetime of 26.5(5.3) days, the transition from this metastable state to the ground state bears a quality factor of 1.1×1023 and allows for the construction of a HCI clock with a fractional frequency instability of <10−19/√τ.
K. Kromer, C. Lyu, M. Door, P. Filianin, Z. Harman, J. Herkenhoff, P. Indelicato, C. H. Keitel, D. Lange, Y. N. Novikov, C. Schweiger, S. Eliseev, K. Blaum, “Observation of a Low-Lying Metastable Electronic State in Highly Charged Lead by Penning-Trap Mass Spectrometry”, Phys. Rev. Lett. 131, 223002 (2023).
https://journals.aps.org/prl/abstract/10.1103/PhysRevLett.131.223002
Related to Project B01, B02
Abstract:
Numerical simulations of the full quantum properties of interacting many-body systems by means of field-theoretic Monte Carlo techniques are often limited due to a sign problem. Here we simulate properties of a dilute two-dimensional Bose gas in the vicinity of the Berezinskii-Kosterlitz-Thouless (BKT) transition by means of the complex Langevin (CL) algorithm, thereby extending our previous CL study of the three-dimensional Bose gas to the lower-dimensional case. The purpose of the paper is twofold. On the one hand, it adds to benchmarking of the CL method and thus contributes to further exploring the range of applicability of the method. With the respective results, the universality of the equation of state is recovered, as well as the long-wave-length power-law dependence of the single-particle momentum spectrum below the BKT transition. Analysis of the rotational part of the current density corroborates vortex unbinding in crossing the transition. Beyond these measures of consistency we compute quantum corrections to the critical density and chemical potential in the weakly coupled regime. Our results show a shift of these quantities to lower values as compared to those obtained from classical field theory. It points in the opposite direction as compared to the shift of the critical density found by means of the path-integral Monte Carlo method at larger values of the coupling. Our simulations widen the perspective for precision comparisons with experiment.
P. Heinen, T. Gasenzer, „Simulating the Berezinskii-Kosterlitz-Thouless transition with the complex Langevin algorithm“, Phys. Rev. A 108, 053311 (2023).
https://journals.aps.org/pra/abstract/10.1103/PhysRevA.108.053311
Related to Project A04
Abstract:
Isolated many-body systems far from equilibrium may exhibit scaling dynamics with universal exponents indicating the proximity of the time evolution to a nonthermal fixed point. We find universal dynamics connected with the occurrence of extreme wave excitations in the mutually coupled magnetic components of a spinor gas which propagate in an effectively random potential. The frequency of these rogue waves is affected by the time-varying spatial correlation length of the potential, giving rise to an additional exponent δc≃1/3 for temporal scaling, which is different from the exponent βV≃1/4 characterizing the scaling of the correlation length ℓV∼tβV in time. As a result of the caustics, i.e., focusing events, real-time instanton defects appear in the Larmor phase of the spin-1 system as vortices in space and time. The temporal correlations governing the instanton occurrence frequency scale as tδI. This suggests that the universality class of a nonthermal fixed point could be characterized by different, mutually related exponents defining the evolution in time and space, respectively. Our results have a strong relevance for understanding pattern coarsening from first principles and potential implications for dynamics ranging from the early Universe to geophysical dynamics and microphysics.
I. Siovitz, S. Lannig, Y. Deller, H. Strobel, M.K. Oberthaler, T. Gasenzer, “Universal Dynamics of Rogue Waves in a Quenched Spinor Bose Condensate”, Phys. Rev. Lett. 131, 183402 (2023).
https://journals.aps.org/prl/abstract/10.1103/PhysRevLett.131.183402
Related to Project A04, A07
Abstract:
We demonstrate the applicability and advantages of Discontinuous Galerkin (DG) schemes in the context of the Functional Renormalization Group (fRG). We investigate the -model in the large limit. It is shown that the flow equation for the effective potential can be cast into a conservative form. We discuss results for the Riemann problem, as well as initial conditions leading to a first and second order phase transition. In particular, we unravel the mechanism underlying first order phase transitions, based on the formation of a shock in the derivative of the effective potential.
E. Grossi, N. Wink, „Resolving phase transitions with discontinuous Galerkin methods“, SciPost
Phys. Core 6, 071 (2023).
https://scipost.org/10.21468/SciPostPhysCore.6.4.071
Related to Project B01
Abstract:
Optical frequency metrology in atoms and ions can probe hypothetical fifth forces between electrons and neutrons by sensing minute perturbations of the electronic wave function induced by them. A generalized King plot has been proposed to distinguish them from possible standard model effects arising from, e.g., finite nuclear size and electronic correlations. Additional isotopes and transitions are required for this approach. Xenon is an excellent candidate, with seven stable isotopes with zero nuclear spin, however it has no known visible ground-state transitions for high resolution spectroscopy. To address this, we have found and measured twelve magnetic-dipole lines in its highly charged ions and theoretically studied their sensitivity to fifth forces as well as the suppression of spurious higher-order standard model effects. Moreover, we identified at 764.8753(16) nm a E2-type ground-state transition with 500 s excited state lifetime as a potential clock candidate further enhancing our proposed scheme.
N.-H. Rehbehn, M. K. Rosner, J. C. Berengut, P. O.Schmidt, T. Pfeifer, M. F. Gu, J. R. C.
López-Urrutia, „Narrow and Ultranarrow Transitions in Highly Charged Xe Ions as Probes of
Fifth Forces“, Phys. Rev. Lett. 131, 161803 (2023).
https://journals.aps.org/prl/abstract/10.1103/PhysRevLett.131.161803
Related to Project B01, B02
Abstract:
The hadronic vacuum polarization correction to the 𝑔 factor of a bound electron is investigated theoretically. An effective hadronic Uehling potential obtained from measured cross sections of 𝑒−𝑒+ annihilation into hadrons is employed to calculate 𝑔-factor corrections for low-lying hydrogenic levels. Analytical Dirac-Coulomb wave functions, as well as bound wave functions accounting for the finite nuclear radius are used. Closed formulas for the 𝑔-factor shift in the case of a point-like nucleus are derived. In heavy ions, such effects are found to be much larger than for the free-electron 𝑔 factor.
E. Dizer, Z. Harman, „Hadronic vacuum polarization correction to the bound-electron g factor“,
Phys. Rev. A 108, 042808 (2023).
https://journals.aps.org/pra/abstract/10.1103/PhysRevA.108.042808
Related to Project B02
Abstract:
The increasingly high accuracy of top-quark studies at the LHC calls for a theoretical description of t \bar{t} production and decay in terms of exact matrix elements for the full 2 → 6 process that includes the off-shell production and the chain decays of t \bar{t} and tW intermediate states, together with their quantum interference. Corresponding NLO QCD calculations matched to parton showers are available for the case of dileptonic channels and are implemented in the bb4l Monte Carlo generator, which is based on the resonance-aware POWHEG method. In this paper, we present the first NLOPS predictions of this kind for the case of semileptonic channels. In this context, the interplay of off-shell t \bar{t} + tW production with various other QCD and electroweak subprocesses that yield the same semileptonic final state is discussed in detail. On the technical side, we improve the resonance-aware POWHEG procedure by means of new resonance histories based on matrix elements, which enable a realistic separation of t \bar{t} and tW contributions. Moreover, we introduce a general approach which makes it possible to avoid certain spurious terms that arise from the perturbative expansion of decay widths in any off-shell higher-order calculation, and which are large enough to jeopardise physical finite-width effects. These methods are implemented in a new version of the bb4l Monte Carlo generator, which is applicable to all dileptonic and semileptonic channels, and can be extended to fully hadronic channels. The presented results include a NLOPS comparison of off-shell against on-shell t \bar{t} + tW production and decay, where we highlight various non-trivial aspects related to NLO and parton-shower radiation in leptonic and hadronic top decays.
T. Jezo, J. M. Lindert, S. Pozzorini, „Resonance-aware NLOPS matching for off-shell t\bar{t} + tW
production with semileptonic decays“, JHEP 10, 008 (2023).
https://link.springer.com/article/10.1007/JHEP10(2023)008
Related to Project C05
Abstract:
Closed quantum systems far from thermal equilibrium can show universal dynamics near attractor solutions, known as non-thermal fixed points, generically in the form of scaling behaviour in space and time. A systematic classification and comprehensive understanding of such scaling solutions are tasks of future developments in non-equilibrium quantum many-body theory. In this tutorial review, we outline several analytical approaches to non-thermal fixed points and summarise corresponding numerical and experimental results. The analytic methods include a non-perturbative kinetic theory derived within the two-particle irreducible effective action formalism, as well as a low-energy effective field theory framework. As one of the driving forces of this research field are numerical simulations, we summarise the main results of exemplary cases of universal dynamics in ultracold Bose gases. This encompasses quantum vortex ensembles in turbulent superfluids as well as recently observed real-time instanton solutions in one-dimensional spinor condensates.
A. N. Mikheev, I. Siovitz, T. Gasenzer, „Universal dynamics and non-thermal fixed points in
quantum fluids far from equilibrium“, Eur. Phys. J. Spec. Top. (2023).
https://link.springer.com/article/10.1140/epjs/s11734-023-00974-7
Related to Project A04
Abstract:
The emergence of patterns from simple physical laws belongs to the most striking topics in natural science. In particular, the spontaneous formation of structures from an initially homogeneous state can eventually lead to stable, non-homogeneous states of matter. Here we report on the spontaneous formation of square lattice patterns in a rotationally symmetric and driven Bose-Einstein condensate, confined in a two-dimensional box potential with absorptive boundaries. The drive is realized by globally modulating the two-particle interaction periodically in time. After a primary phase of randomly oriented stripes that emerge as a consequence of the Faraday instability, we observe the subsequent formation of persistent square lattice patterns in the highly occupied regime, where phonon-phonon interactions become relevant. We show theoretically that this state can be understood as an attractive fixed point of coupled nonlinear amplitude equations. Establishing the existence of this fixed point opens the perspective for engineering new, highly correlated states of matter in driven superfluids.
N. Liebster, M. Sparn, E. Kath, K. Fujii, S. Görlitz, T. Enss, H. Strobel, M. K. Oberthaler, “Spontaneous formation of persistent square pattern in a driven superfluid”, Sept. 7, 2023, arXiv:2309.03792 (2023).
https://arxiv.org/abs/2309.03792
Related to Project A04, C02, C03
Abstract:
Nuclear parton distribution functions (nPDFs) are crucial in studying nuclear structure and high-energy nuclear collisions. nPDFs have been determined via ‘global QCD analyses’, in which the nPDF-dependent predictions for a given process are compared with their actual measurements. One of the challenging parts of nPDF extractions is the estimation of uncertainties. The most common approach for this purpose is the Hessian method, which, however, has certain shortcomings, especially in the case of weaker data constraints. Here, we will show a case study for an alternative approach where nPDF uncertainties are estimated using Markov Chain Monte Carlo (MCMC) methods.
N. Derakhshanian, P. Risse, T. Ježo, M. Klasen, K. Kovařík, A. Kusina, F. I. Olness, I. Schienbein,
„Nuclear PDF Determination Using Markov Chain Monte Carlo Methods“, Acta Phys.
Polon. Supp. 16, 7 (2023).
https://www.actaphys.uj.edu.pl/index_n.php?I=S&V=16&N=7#A33
Related to Project C05
Abstract:
We investigate the excitation spectrum and compressibility of a dipolar Bose-Einstein condensate in an infinite tube potential in the parameter regime where the transition between superfluid and supersolid phases occurs. Our study focuses on the density range in which crystalline order develops continuously across the transition. Above the transition the superfluid shows a single gapless excitation band, phononic at small momenta and with a roton at a finite momentum. Below the transition, two gapless excitations branches (three at the transition point) emerge in the supersolid. We examine the two gapless excitation bands and their associated speeds of sound in the supersolid phase. Our results show that the speeds of sound and the compressibility are discontinuous at the transition, indicating a second-order phase transition. These results provide valuable insights into the identification of supersolid phenomena in dipolar quantum gases and the relationship to supersolidity in spin-orbit coupled gases.
P. B. Blakie, L. Chomaz, D. Baillie, F. Ferlaino, “Compressibility and speeds of sound across the superfluid-to-supersolid phase transition of an elongated dipolar gas”, Phys. Rev. Res. 5, 033161 (2023).
https://journals.aps.org/prresearch/abstract/10.1103/PhysRevResearch.5.033161
Related to Project A07
Abstract:
A method to calculate hadron momentum spectra after feed down from resonance decays in the context of ultra-relativistic heavy ion collisions described by relativistic fluid dynamics is presented. The conceptual setup uses the Cooper-Frye freeze-out integration together with an integral operator describing resonance decays. We provide explicit expressions for the integration over the freeze-out surface for a smooth and symmetric background solution, as well as for linearized perturbations around it. A major advantage of our method is that many integrals can be precomputed independently of a concrete hydrodynamic simulation. Additionally, we examine the influence of adding heavier resonances to the decay chain on the spectrum of pions and show how to include a phase with partial chemical equilibrium in order to separate the chemical from the kinetic freeze-out.
A. Kirchner, E. Grossi, S. Floerchinger, “Cooper-Frye spectra of hadrons with viscous corrections including feed down from resonance decays”, Aug. 21, 2023, arXiv:2308.10616 (2023).
https://arxiv.org/abs/2308.10616
Related to Project C06
Abstract:
Exploiting a mapping between transport theory and fluid dynamics, we show how a fluid-dynamic description of the diffusion of charm quarks in the QCD plasma is feasible. We show results for spectra of charmed hadrons obtained with a fluid-dynamic description of the quark-gluon plasma (QGP) coupled with the conservation of a heavy-quark – antiquark current. We compare our calculations with the most recent experimental data in order to provide further constraints on the transport coefficients of the QGP.
F. Capellino, A. Dubla, S. Floerchinger, E. Grossi, A. Kirchner, S. Masciocchi, “Momentum distribution of charm hadrons in a fluid-dynamic approach”, July 28, 2023, arXiv:2307.15580 (2023).
https://arxiv.org/abs/2307.15580
Related to Project A02
Abstract:
Mass-dependent quark contributions are of great importance to DIS processes. The simplified-ACOT-scheme includes these effects over a wide range of momentum transfers up to next-to-leading order in QCD. In recent years an improvement in the case of neutral current DIS has been achieved by using zero-mass contributions up to next-to-next-to-leading order (NNLO) with massive phase-space constraints. In this work, we extend this approach to the case of charged current DIS and provide an implementation in the open-source code APFEL++. The increased precision will be valuable for ongoing and future neutrino programs, the Electron-Ion-Collider and the studies of partonic substructure of hadrons and nuclei. A highly efficient implementation using gridding techniques extends the applicability of the code to the determination of parton distribution functions (PDFs).
P. Risse, V. Bertone, T. Ježo, M. Klasen, K. Kovařík, F.I. Olness, I. Schienbein, „Fast evaluation
of heavy-quark contributions to DIS in APFEL++“, 17. Juli 2023, arXiv:2307.08269 (2023).
https://arxiv.org/abs/2307.08269
Related to Project C05
Abstract:
We discuss the foundation for a new global nCTEQ nuclear PDF analysis, combining a number of our previous analyses into one consistent framework with updates to the underlying theoretical treatment as well as the addition of new available data. In particular, the new global release will be the first nCTEQ release containing neutrino DIS scattering data in a consistent manner together with JLab high-x DIS data and new LHC p-Pb data. These additions will improve the data-driven description of nuclear PDFs in new regions, especially the strange quark and the gluon PDF at low-x.
P. Risse, N. Derakhshanian, P. Duwentäster, T. Ježo, C. Keppel, M. Klasen, K. Kovařík,
A.Kusina, C. Léger, J.G.Morfín, F.I. Olness, R. Ruiz, I. Schienbein, J.Y. Yu, „Towards a New
nCTEQ global nPDF release“, 15. Juli 2023, arXiv:2307.07814 (2023).
https://arxiv.org/abs/2307.07814
Related to Project C05
Abstract:
Inner-shell electrons naturally sense the electric field close to the nucleus, which can reach extreme values beyond 1015V/cm for the innermost electrons. Especially in few-electron highly charged ions, the interaction with the electromagnetic fields can be accurately calculated within quantum electrodynamics (QED), rendering these ions good candidates to test the validity of QED in strong fields. Consequently, their Lamb shifts were intensively studied in the last decades. Another approach is the measurement of g factors in highly charged ions. However, so far, either experimental accuracy or small field strength in low-Z ions limited the stringency of these QED tests. Here, we report on our high-precision, high-field test of QED in hydrogenlike 118Sn49+. The highly charged ions were produced with the Heidelberg-EBIT (electron beam ion trap) and injected into the ALPHATRAP Penning-trap setup, where the bound-electron g factor was measured with a precision of 0.5 parts-per-billion. For comparison, we present state-of-the-art theory calculations, which together test the underlying QED to about 0.012%, yielding a stringent test in the strong-field regime. With this measurement, we challenge the best tests via the Lamb shift and, with anticipated advances in the g-factor theory, surpass them by more than an order of magnitude.
J. Morgner, B. Tu, C. M. König, T. Sailer, F. HeiSSe, H. Bekker, B. Sikora, C. Lyu, V. A. Yerokhin, Z. Harman, J. R. Crespo López-Urrutia, C. H. Keitel, S. Sturm, K. Blaum, “Stringent test of QED with hydrogenlike tin”, July 13, 2023, arXiv:2307.06613 (2023).
https://arxiv.org/abs/2307.06613
Related to Project B01
Abstract:
Close to equilibrium, the underlying symmetries of a system determine its possible universal behavior. Far from equilibrium, however, different universal phenomena associated with the existence of multiple non-thermal fixed points can be realized for given microscopic symmetries. Here, we study this phenomenon using a quasi-one-dimensional spinor Bose-Einstein condensate. We prepare two different initial conditions and observe two distinct universal scaling dynamics with different exponents. Measurements of the complex-valued order parameter with spatial resolution allow us to characterize the phase-amplitude excitations for the two scenarios. Our study provides new insights into the phenomenon of universal dynamics far from equilibrium and opens a path towards mapping out the associated basins of non-thermal fixed points.
S. Lannig, M. Prüfer, Y. Deller, I. Siovitz, J. Dreher, T. Gasenzer, H. Strobel, M. K. Oberthaler,
„Observation of two non-thermal fixed points for the same microscopic symmetry“, 28. Juni
2023, arXiv:2306.16497 (2023).
https://arxiv.org/abs/2306.16497
Related to Project A04
Abstract:
We develop an innovative and unbiased procedure, based on event mixing, to account for unavoidable contributions from volume (or system size) fluctuations to experimentally measured moments of particle multiplicity distributions produced in relativistic nuclear collisions. Within the wounded-nucleon model they are characterized by fluctuations of the number of wounded nucleons, the latter usually referred to as participants. For the first time we extract participant fluctuations directly from the data used for the fluctuation analysis, i.e., without involving model calculations. To achieve this we constructed a dedicated event-mixing algorithm that eliminates all possible correlations between produced particles while preserving the volume fluctuations. The procedure provides direct access to the cumulants of wounded-nucleon distributions, which can be used to account for non-critical contributions to the experimentally measured cumulants of multiplicity distributions.
A. Rustamov, R. Holzmann, J. Stroth, „A model-free procedure to correct for volume fluctuations
in E-by-E analyses of particle multiplicities“, Nucl. Phys. A 1034, 122641 (2023).
https://www.sciencedirect.com/science/article/abs/pii/S0375947423000441
Related to Project A01
Abstract:
We present a method to calculate the natural line width and energy dependent line shape due to fluorescence decay of core excited atoms within a full relativistic multi-reference configuration interaction theory. The atomic absorption lines show a deviation from a Lorentzian line-shape due to energy dependent matrix elements of the localized electronic state coupling to the photon field. This gives rise to spectral lines with small but visible asymmetry. One generally finds an excess of spectral weight at the high energy shoulder of the atomic absorption line. We present the example of nuclear decay of 55Fe by electron capture of an inner-shell core electron. We show that the amount of ionizing radiation in the energy window between 50 and 200 keV is around one order of magnitude larger due to the energy dependent fluorescence yield lifetime compared to the value one would obtain if one assumes a constant fluorescence decay rate. This yields a total change of energy deposited into ionizing radiation of about 1\textperthousand. Our calculations are in good agreement with previous calculations and experimental observations where data is available. Our results can be further validated by high precision measurements of electron capture nuclear decay spectra using recently developed experimental methods.
M. Merstorf, M. Braß, M. W. Haverkort, „Non-Lorentzian atomic natural line-shape of core
level multiplets: Access high energy x-ray photons in electron capture nuclear decay“, 14. Juni 2023, arXiv:2307.13812 (2023).
https://arxiv.org/abs/2307.13812
Related to Project B01, C01
Abstract:
State-of-the-art hydrodynamic simulations of the quark-gluon plasma are unable to reproduce the elliptic flow of particles observed at the BNL Relativistic Heavy Ion Collider (RHIC) in relativistic 238U+238U collisions when they rely on information obtained from low-energy experiments for the implementation of deformation in the colliding 238U ions. We show that this is due to an inappropriate treatment of well-deformed nuclei in the modeling of the initial conditions of the quark-gluon plasma. Past studies have identified the deformation of the nuclear surface with that of the nuclear volume, though these are different concepts. In particular, a volume quadrupole moment can be generated by both a surface hexadecapole and a surface quadrupole moment. This feature was so far neglected in the modeling of heavy-ion collisions, and is particularly relevant for nuclei like 238U, which is both quadrupole deformed and hexadecapole deformed. With rigorous input from Skyrme density functional calculations, we show that correcting for such effects in the implementation of nuclear deformations in hydrodynamic simulations restores agreement with BNL RHIC data. This brings consistency to the results of nuclear experiments across energy scales, and demonstrates the impact of the hexadecapole deformation of 238U on high-energy collisions.
W. Ryssens, G. Giacalone, B. Schenke, C. Shen, “Evidence of Hexadecapole Deformation in Uranium-238 at the Relativistic Heavy Ion Collider”, Feb. 27, 2023, Phys. Rev. Lett. 130, 212302, (2023).
https://journals.aps.org/prl/abstract/10.1103/PhysRevLett.130.212302
Related to Project C06
Abstract:
We investigate signal propagation in a quantum field simulator of the Klein–Gordon model realized by two strongly coupled parallel one-dimensional quasi-condensates. By measuring local phononic fields after a quench, we observe the propagation of correlations along sharp light-cone fronts. If the local atomic density is inhomogeneous, these propagation fronts are curved. For sharp edges, the propagation fronts are reflected at the system’s boundaries. By extracting the space-dependent variation of the front velocity from the data, we find agreement with theoretical predictions based on curved geodesics of an inhomogeneous metric. This work extends the range of quantum simulations of nonequilibrium field dynamics in general space–time metrics.
M. Tajik, M. Gluza, N. Sebe, P. Schüttelkopf, F. Cataldini, J. Sabino, F. Møller, S.-C. Ji,
S. Erne, G. Guarnieri, S. Sotiriadis, J. Eisert, J. Schmiedmayer, “Experimental observation of curved light-cones in a quantum field simulator”, PNAS 120, (2023).
https://www.pnas.org/doi/10.1073/pnas.2301287120
Related to Project A03
Abstract:
We present our experimental and theoretical framework, which combines a broadband superluminescent diode with fast learning algorithms to provide speed and accuracy improvements for the optimization of on-dimensional optical dipole potentials, here generated with a digital micromirror device. To characterize the setup and potential speckle patterns arising from coherence, we compare the superluminescent diode to a single-mode laser by investigating interference properties. We employ machine-learning tools to train a physics-inspired model acting as a digital twin of the optical system predicting the behavior of the optical apparatus including all its imperfections. Implementing an iterative algorithm based on iterative learning control we optimize optical potentials an order of magnitude faster than heuristic optimization methods. We compare iterative model-based “offline” optimization and experimental feedback-based “online” optimization. Our methods provide a route to fast optimization of optical potentials, which is relevant for the dynamical manipulation of ultracold gases.
M. Calzavara, Y. Kuriatnikov, A. Deutschmann-Olek, F. Motzoi, S. Erne, A. Kugi, T. Calarco, J. Schmiedmayer, M. Prüfer, “Optimizing Optical Potentials With Physics-Inspired Learning Algorithms”, Phys. Rev. Appl. 19 (2023).
https://journals.aps.org/prapplied/abstract/10.1103/PhysRevApplied.19.044090
Related to Project A03
Abstract:
The theoretical understanding of scaling laws of entropies and mutual information has led to substantial advances in the study of correlated states of matter, quantum field theory and gravity. Experimentally measuring von Neumann entropy in quantum many-body systems is challenging, as it requires complete knowledge of the density matrix, which normally requires the implementation of full state reconstruction techniques. Here we measure the von Neumann entropy of spatially extended subsystems in an ultracold atom simulator of one-dimensional quantum field theories. We experimentally verify one of the fundamental properties of equilibrium states of gapped quantum many-body systems—the area law of quantum mutual information. We also study the dependence of mutual information on temperature and on the separation between the subsystems. Our work represents a step towards employing ultracold atom simulators to probe entanglement in quantum field theories.
M. Tajik, I. Kukuljan, S. Sotiriadis, B. Rauer, T. Schweigler, F. Cataldini, J. Sabino, F. Møller, P. Schüttelkopf, Si-Cong Ji, D. Sels, E. Demler, J. Schmiedmayer, “Experimental verification of the area law of mutual information in a quantum field simulator”, Nature Phys. 19 (2023).
https://www.nature.com/articles/s41567-023-02027-1
Related to Project A03
Abstract:
Having a detailed theoretical knowledge of the low-energy structure of the heavy odd-mass nucleus 197Au is of prime interest as the structure of this isotope represents an important input to theoretical simulations of collider experiments involving gold ions performed at relativistic energies. In the present article, therefore, we report on new results on the structure of 197Au obtained from state-of-the-art multi-reference energy density functional (MR-EDF) calculations. Our MR-EDF calculations were realized using the Skyrme-type pseudo-potential SLyMR1, and include beyond mean-field correlations through the mixing, in the spirit of the Generator Coordinate Method (GCM), of particle-number and angular-momentum projected triaxially deformed Bogoliubov quasi-particle states. Comparison with experimental data shows that the model gives a reasonable description of 197Au with in particular a good agreement for most of the spectroscopic properties of the 3/2+1 ground state. From the collective wave function of the correlated state, we compute an average deformation β¯(3/2+1)=0.13 and γ¯(3/2+1)=40∘ for the ground state. We use this result to construct an intrinsic shape of 197Au representing a microscopically-motivated input for precision simulations of the associated collider processes. We discuss, in particular, how the triaxiality of this nucleus is expected to impact 197Au+197Au collision experiments at ultrarelativistic energy.
B. Bally, G. Giacalone, M. Bender, “The shape of gold”, Eur. Phys. J. A 59, 58 (2023).
https://link.springer.com/article/10.1140/epja/s10050-023-00955-3
Related to Project C06
Abstract:
We present the first direct and nonperturbative computation of the graviton spectral function in quantum gravity. This is achieved with the help of a novel Lorentzian renormalization group approach, combined with a spectral representation of correlation functions. We find a positive graviton spectral function, showing a massless one-graviton peak and a multigraviton continuum with an asymptotically safe scaling for large spectral values. We also study the impact of a cosmological constant. Further steps to investigate scattering processes and unitarity in asymptotically safe quantum gravity are indicated.
J. Fehre, D. F. Litim, J. M. Pawlowski, M. Reichert, “Lorentzian Quantum Gravity and the Graviton Spectral Function”, Phys.Rev.Lett. 130 (2023).
https://journals.aps.org/prl/abstract/10.1103/PhysRevLett.130.081501
Related to Project A02
Abstract:
Fluid dynamic considerations are used to determine the electric current spectral density in the regime of small energies and momenta. The spectral density in this regime is parameterized by the electric conductivity, the charge susceptibility, and the relaxation time for the electric current, which is needed for relativistic causality. Experimentally, the spectral function can be accessed through the production rates of photons and dileptons in the expanding quark-gluon plasma. We use fluid dynamic simulations of high energy nuclear collisions, together with the transport limit of the spectral density, to obtain photon and dielectron spectra for different values of the conductivity and relaxation times. The yields of photon and dileptons produced in the plasma are compared to the background from decays of short-lived hadrons. We discuss how experiments can constrain the electrical conductivity and associated relaxation time of the quark-gluon plasma.
S. Floerchinger, C. Gebhardt, K. Reygers, „Electrical conductivity of the quark-gluon plasma
from the low energy limit of photon and dilepton spectra“, Phys. Lett. B 837, 137647 (2023).
https://www.sciencedirect.com/science/article/pii/S037026932200781X
Related to Project A01
Abstract:
The atomic mass of uranium-238 has been determined to be 238.050787618(15) u, improving the literature uncertainty by two orders of magnitude. It is obtained from a measurement of the mass ratio of 238U47+ and 132Xe26+ ions with an uncertainty of 3.5×10−12. The measurement was carried out with the Penning-trap mass spectrometer Pentatrap and was accompanied by a calculation of the binding energies 𝐸U and 𝐸Xe of the 47 and 26 missing electrons of the two highly charged ions, respectively. These binding energies were determined using an ab initio multiconfiguration Dirac-Hartree-Fock method to be 𝐸U=39927(10) eV and 𝐸Xe=8971.2(21) eV. The new mass value will serve as a reference for high-precision mass measurements in the heavy mass region of the nuclear chart up to transuranium nuclides.
K. Kromer, C. Lyu, J. Biero, M. Door, L. Enzmann, P. Filianin, G. Gaigalas, Z. Harman, J.
Herkenhoff, W. Huang, C. H. Keitel, S. Eliseev, K. Blaum, „Atomic mass determination of
uranium-238“, Phys. Rev. C 109, L021301 (2024).
https://journals.aps.org/prc/abstract/10.1103/PhysRevC.109.L021301
Related to Project B01, B02
Abstract:
The relationship between many-body interactions and dimensionality is integral to numerous emergent quantum phenomena. A striking example is the Bose gas, which upon confinement to one dimension (1D) obeys an infinite set of conservation laws, prohibiting thermalization and constraining dynamics. In our experiment, we demonstrate that such a 1D behavior can extend much further into the dimensional crossover toward 3D than expected. Starting from a weakly interacting Bose gas trapped in a highly elongated potential, we perform a quench to instigate the dynamics of a single density mode. Employing the theory of generalized hydrodynamics, we identify the dominant relaxation mechanism as the 1D dephasing of the relevant collective excitations of the system, the rapidities. Surprisingly, the dephasing remains dominant even for temperatures far exceeding conventional limits of one dimensionality where thermalization should occur. We attribute our observations to an emergent Pauli blocking of transverse excitations caused by the rapidities assuming fermionic statistics, despite the gas being purely bosonic. Thus, our study suggests that 1D physics is less fragile than previously thought, as it can persist even in the presence of significant perturbations. More broadly, by employing the exact Bethe ansatz solutions of the many-body system, we facilitate an interpretation of how the emergent macroscopic behavior arises from the microscopic interactions.
F. Cataldini, F. Møller, M. Tajik, J. Sabino, S.-C. Ji, I. Mazets, T. Schweigler, B. Rauer, J.
Schmiedmayer, “Emergent Pauli Blocking in a Weakly Interacting Bose Gas”, Phys. Rev. X 12 (2022).
https://journals.aps.org/prx/abstract/10.1103/PhysRevX.12.041032
Related to Project A03
Abstract:
Electromagnetic probes are not affected by hadronization and provide
direct information about the space-time evolution of high-energy nucleus–
nucleus collisions. In particular, the measurement of thermal radiation
from the quark–gluon plasma and the extraction of an effective medium
temperature belong to the key objectives in heavy-ion physics. We provide
a brief tour of current results and an outlook on future measurements.
K. Reygers, „Experimental Overview of Electromagnetic Probes in Ultra-relativistic Nucleus-
Nucleus Collisions“, Acta Phys. Polon. Supp. 16, 1 (2022).
https://www.actaphys.uj.edu.pl/index_n.php?I=S&V=16&N=1#A19
Related to Project A01
Abstract:
Predictions are presented within the framework of the statistical hadronization model for integrated yields of bottomonia in Pb–Pb collisions at the LHC. We investigate the centrality dependence of Υ production and provide predictions for a large set of still-unmeasured open-beauty hadrons.
A. Andronic, P. Braun-Munzinger, K. Redlich, J. Stachel, “Statistical Hadronization of b-quarks in PbPb Collisions at LHC Energy: A Case for Partial Equilibration of b-quarks?”, Acta Phys. Polon. Supp. 16, 1 (2022).
https://www.actaphys.uj.edu.pl/index_n.php?I=S&V=16&N=1#A107
Related to Project C05, A01, A02, C06
Abstract:
High-performance graphical processing units (GPU) are used for the repeated parallelised
propagation of non-linear partial differential equations on large spatio-temporal grids. The main
challenge results as a combination of the requirement of large grids for exploring scaling over
several orders of magnitude, both in space and time, and the need for high statistics in
averaging over many runs, in computing correlation functions for highly fluctuating quantum
many-body states. With our simulations, we explore the dynamics of complex quantum
systems far from equilibrium, with the aim of classifying their universal characteristics such as
scaling exponents near non-thermal fixed points. Our results are strongly relevant for
the development of synthetic quantum systems when exploring the respective physics in the
laboratory.
I. Siovitz, P. Heinen, N. Rasch, S. Lannig, Y. Deller, H. Strobel, M. Oberthaler, T. Gasenzer,
„Universal Dynamics at the Lowest Temperatures“, Proc. 8th bwHPC Sympos. 2022, 51 (2022).
https://elib.uni-stuttgart.de/items/b4ae0d25-14e1-4ce9-aca2-1e9cbb31cb81
Related to Project A04
Abstract:
We discuss the emergence of a low-energy effective theory with quarks, mesons, diquarks and baryons at vanishing and finite baryon density from first principle QCD. The present work also includes an overview on diquarks at vanishing and finite density, and elucidates the physics of transitional changes from baryonic matter to quark matter including diquarks. This set-up is discussed within the functional renormalisation group approach with dynamical hadronisation. In this framework it is detailed how mesons, diquarks, and baryons emerge dynamically from the renormalisation flow of the QCD effective action. Moreover, the fundamental degrees of freedom of QCD, quarks and gluons, decouple from the dynamics of QCD below the respective mass gaps. The resulting global picture unifies the different low energy effective theories used for low and high densities within QCD, and allows for a determination of the respective low energy constants directly from QCD.
K. Fukushima, J. M. Pawlowski, N. Strodthoff, “Emergent Hadrons and Diquarks”, Annals Phys. 446, 169106 (2022).
https://www.sciencedirect.com/science/article/pii/S0003491622002093?via%3Dihub
Related to Project A02
Abstract:
This document describes the plans of the ALICE Collaboration for a major upgrade of its detector, referred to as ALICE 3, which is proposed for physics data-taking in the LHC Run 5 and beyond. ALICE 3 will enable an extensive programme to fully exploit the LHC for the study of the properties of strongly interacting matter with high-energy nuclear collisions. The proposed detector layout, based on advanced silicon sensors, features superb pointing resolution, excellent tracking and particle identification over a large acceptance and high readout-rate capabilities. This document discusses the proposed physics programme, the detector concept, and its physics performance for a suite of benchmark measurements.
ALICE Collaboration, “Letter of intent for ALICE 3: A next-generation heavy-ion experiment
at the LHC”, Nov. 4, 2022, arXiv:2211.02491 (2022).
https://arxiv.org/abs/2211.02491
Related to Project A01, C06
Abstract:
We compute high-order baryon number fluctuations at finite temperature and density within a QCD-assisted low energy effective field theory. Quantum, thermal and density fluctuations are incorporated with the functional renormalization group approach. Quantum and in-medium fluctuations are encoded via the evolution of renormalization group flow equations. The resulting fourth- and sixth-order baryon number fluctuations meet the lattice benchmark results at vanishing density. They are consistent with experimental measurements, and in particular, the non-monotonic dependence of the kurtosis of net-baryon number distributions on the collision energy is observed in our calculations. This non-monotonicity arises from the increasingly sharpened chiral crossover with the decrease of collision energy.
W. Fu, X. Luo, J. M. Pawlowski, F. Rennecke, R. Wen, S. Yin, “High-order baryon number
fluctuations within the fRG approach”, PoS CPOD2021, 009 (2022).
Related to Project A02
Abstract:
In this work, I calculate the resolved spectra for the three stages of the bottom-up scenario, which are comparable to the thermal contribution, particularly at higher values of the saturation scale . Analytical solutions are obtained by including a parametrization of scaling solutions from far-from-equilibrium classical statistical lattice simulations into a small angle kinetic rate. Furthermore, a theoretically motivated ansatz is used to account for near-collinear enhancement of the low- radiation. The system is phenomenologically constrained using the charged hadron multiplicities from LHC and RHIC as in previous parametric estimates and fair agreement with the data available for photons was found. I find that for this realistic set of parameters, the contribution from the pre-equilibrium dominates the excess photons.
O. Garcia-Montero, “Non-equilibrium photons from the bottom-up thermalization scenario”, Annals Phys. 443, 168984 (2022).
https://www.sciencedirect.com/science/article/abs/pii/S0003491622001403?via%3Dihub
Related to Project
Abstract:
A central question in high-energy nuclear phenomenology is how the geometry of the quark-gluon plasma (QGP) formed in relativistic nuclear collisions is precisely shaped. In our understanding of such processes, two features are especially crucial for the determination of the QGP geometry, respectively, the nucleon size and the energy deposition scheme. This contribution reports on the (circular) evolution of such features in state-of-the-art model incarnations of heavy-ion collisions over the past seven years. Ideas for future directions of investigation are pointed out.
G. Giacalone, “There and Sharp Again: The Circle Journey of Nucleons and Energy Deposition”, Aug. 14, arXiv:2208.06839, (2023).
https://arxiv.org/abs/2208.06839
Related to Project C06
Abstract:
Vector boson production and neutrino deep-inelastic scattering (DIS) data are crucial for constraining the strange quark parton distribution function (PDF) and more generally for flavor decomposition in PDF extractions. We extend the nCTEQ15 nuclear PDFs (nPDFs) by adding the recent and production data from the LHC in a global nPDF fit. The new nPDF set, referred to as nCTEQ15WZ, is used as a starting point for a follow-up study in which we assess the compatibility of neutrino DIS data with charged lepton DIS data. Specifically, we re-analyze neutrino DIS data from NuTeV, Chorus, and CDHSW, as well as dimuon data from CCFR and NuTeV. To scrutinize the level of compatibility, different kinematic regions of the neutrino data are investigated. Fits to the neutrino data alone and a preliminary global fit are performed and compared to nCTEQ15WZ.
K. F. Muzakka, P. Duwentäster, T. J. Hobbs, T. Jeo, M. Klasen, K. Kovaík, A. Kusina, J. G.
Morfín, F. I. Olness, R. Ruiz, I. Schienbein, J. Y. Yu, “Impact of W and Z Production Data
and Compatibility of Neutrino DIS Data in Nuclear Parton Distribution Functions”, SciPost Phys Proc. 8, 041, (2022).
https://scipost.org/10.21468/SciPostPhysProc.8.041
Related to Project C05
Abstract:
Near the second order phase transition point, QCD with two flavours of massless quarks can be approximated by an O(4) model, where a symmetry breaking external field H can be added to play the role of quark mass.
The Lee-Yang theorem states that the equation of state in this model has a branch cut along the imaginary H axis for |Im[H]|>Hc, where Hc indicates a second order critical point.
This point, known as Lee-Yang edge singularity, is of importance to the thermodynamics of the system.
We report here on ongoing work to determine the location of Hc via complex Langevin simulations.
F. Attanasio, M. Bauer, L. Kades, J. M. Pawlowski, “Searching for Yang-Lee zeros in O(N)
models”, PoS LATTICE2021, 223 (2022).
Related to Project A02
Abstract:
We determine the chiral phase structure of (2+1)-flavor QCD in dependence of temperature and the light flavor quark mass with Dyson-Schwinger equations. Specifically, we compute the renormalized chiral condensate and its susceptibility. The latter is used to determine the (pseudo)critical temperature for general light current quark masses. In the chiral limit we obtain a critical temperature of about 141 MeV. This result is in quantitative agreement with recent functional renormalization group results in QCD and is compatible with the respective lattice results. We also compute the order parameter potential of the light chiral condensate, map out the regime in the phase diagram which exhibits quasi-massless modes, and discuss the respective chiral dynamics.
F. Gao, J. M. Pawlowski, “Phase structure of (2+1)-flavor QCD and the magnetic equation of state”, Physical Review D 105, (2022).
https://onlinelibrary.wiley.com/doi/full/10.1002/piuz.202370204
Related to Project A02
Abstract:
Path integrals with complex actions are encountered for many physical systems ranging from spin- or mass-imbalanced atomic gases and graphene to quantum chromodynamics at finite density to the nonequilibrium evolution of quantum systems. Many computational approaches have been developed for tackling the sign problem emerging for complex actions. Among these, complex Langevin dynamics has the appeal of general applicability. One of its key challenges is the potential convergence of the dynamics to unphysical fixed points. The statistical sampling process at such a fixed point is not based on the physical action and hence leads to wrong predictions. Moreover, its unphysical nature is hard to detect due to the implicit nature of the process. In the present work we set up a general approach based on a Markov chain Monte Carlo scheme in an extended state space. In this approach we derive an explicit real sampling process for generalized complex Langevin dynamics. Subject to a set of constraints, this sampling process is the physical one. These constraints originate from the detailed-balance equations satisfied by the Monte Carlo scheme. This allows us to rederive complex Langevin dynamics from a new perspective and establishes a framework for the explicit construction of new sampling schemes for complex actions.
L. Kades, M. Gärttner, T. Gasenzer, J. M. Pawlowski, “Monte Carlo sampling of complex
actions in extended state spaces”, Phys. Rev. E 105, 045315 (2022).
https://journals.aps.org/pre/abstract/10.1103/PhysRevE.105.045315
Related to Project A02
Abstract:
We reconstruct ghost and gluon spectral functions in 2+1 flavor QCD with Gaussian process regression. This framework allows us to largely suppress spurious oscillations and other common reconstruction artifacts by specifying generic magnitude and length scale parameters in the kernel function. The Euclidean propagator data are taken from lattice simulations with domain wall fermions at the physical point. For the infrared and ultraviolet extensions of the lattice propagators as well as the low-frequency asymptotics of the ghost spectral function, we utilize results from functional computations in Yang-Mills theory and QCD. This further reduces the systematic error significantly. Our numerical results are compared against a direct real-time functional computation of the ghost and an earlier reconstruction of the gluon in Yang-Mills theory. The systematic approach presented in this work offers a promising route toward unveiling real-time properties of QCD.
J. Horak, J. M. Pawlowski, J. Rodríguez-Quintero, J. Turnwald, J. M. Urban, N. Wink, S.
Zafeiropoulos, “Reconstructing QCD spectral functions with Gaussian processes”, Phys. Rev. D 105, (2022).
https://journals.aps.org/prd/abstract/10.1103/PhysRevD.105.036014
Related to Project A02
Abstract:
We reconstruct the Lorentzian graviton propagator in asymptotically safe quantum gravity from Euclidean data. The reconstruction is applied to both the dynamical fluctuation graviton and the background graviton propagator. We prove that the spectral function of the latter necessarily has negative parts similar to, and for the same reasons, as the gluon spectral function. In turn, the spectral function of the dynamical graviton is positive. We argue that the latter enters cross sections and other observables in asymptotically safe quantum gravity. Hence, its positivity may hint at the unitarity of asymptotically safe quantum gravity.
A. Bonanno, T. Denz, J. M. Pawlowski, M. Reichert, “Reconstructing the graviton”, SciPost Phys. 12, 1 (2022).
https://scipost.org/10.21468/SciPostPhys.12.1.001
Related to Project A02, B03, C01
Abstract:
Collective behaviour of final-state hadrons, and multiparton interactions are studied in high-multiplicity ep scattering at a centre-of-mass energy √s = 318 GeV with the ZEUS detector at HERA. Two- and four-particle azimuthal correlations, as well as multiplicity, transverse momentum, and pseudorapidity distributions for charged-particle multiplicities Nch ≥ 20 are measured. The dependence of two-particle correlations on the virtuality of the exchanged photon shows a clear transition from photoproduction to neutral current deep inelastic scattering. For the multiplicities studied, neither the measurements in photoproduction processes nor those in neutral current deep inelastic scattering indicate significant collective behaviour of the kind observed in high-multiplicity hadronic collisions at RHIC and the LHC. Comparisons of PYTHIA predictions with the measurements in photoproduction strongly indicate the presence of multiparton interactions from hadronic fluctuations of the exchanged photon.
[ZEUS collaboration] S. Floerchinger, S. Masciocchi, I. Selyuzhenkov et al., „Azimuthal correlations
in photoproduction and deep inelastic ep scattering at HERA“, JHEP 2021, 102 (2021).
https://link.springer.com/article/10.1007/JHEP12(2021)102
Related to Project C06
Abstract:
A longstanding question in QCD is the origin of the mass gap in the Yang-Mills sector of QCD, i.e., QCD without quarks. In Landau gauge QCD this mass gap, and hence confinement, is encoded in a mass gap of the gluon propagator, which is found both in lattice simulations and with functional approaches. While functional methods are well suited to unravel the mechanism behind the generation of the mass gap, a fully satisfactory answer has not yet been found. In this work we solve the coupled Dyson-Schwinger equations for the ghost propagator, gluon propagator and three-gluon vertex. We corroborate the findings of earlier works, namely that the mass gap generation is tied to the longitudinal projection of the gluon self-energy, which acts as an effective mass term in the equations. Because an explicit mass term is in conflict with gauge invariance, this leaves two possible scenarios: If it is viewed as an artifact, only the scaling solution survives; if it is dynamical, gauge invariance can only be preserved if there are longitudinal massless poles in either of the vertices. We find that there is indeed a massless pole in the ghost-gluon vertex, however in our approximation with the assumption of complete infrared dominance of the ghost this pole is only present for the scaling solution. We also put forward a possible mechanism that may reconcile the scaling solution, with an infrared dominance of the ghost, with the decoupling solutions based on longitudinal poles in the three-gluon vertex as seen in the PT-BFM scheme.
G. Eichmann, J. M. Pawlowski, J. M. Silva, “Mass generation in Landau-gauge Yang-Mills
theory”, Phys. Rev. D 104, 114016 (2021).
https://journals.aps.org/prd/abstract/10.1103/PhysRevD.104.114016
Related to Project A02
Abstract:
In local scalar quantum field theories at finite temperature correlation functions are known to satisfy certain nonperturbative constraints, which for two-point functions in particular implies the existence of a generalization of the standard Källén-Lehmann representation. In this work, we use these constraints in order to derive a spectral representation for the shear viscosity arising from the thermal asymptotic states, η0. As an example, we calculate η0 in ϕ4 theory, establishing its leading behavior in the small and large coupling regimes.
P. Lowdon, R.-A. Tripolt, J. M. Pawlowski, D. H. Rischke, “Spectral representation of the shear viscosity for local scalar QFTs at finite temperature”, Phys. Rev. D 104, 065010 (2021).
https://journals.aps.org/prd/abstract/10.1103/PhysRevD.104.065010
Related to Project A02
Abstract:
We calculate gluon and ghost propagators in Yang-Mills theory in linear covariant gauges. To that end, we utilize Nielsen identities with Landau gauge propagators and vertices as the starting point. We present and discuss numerical results for the gluon and ghost propagators for values of the gauge parameter 0<ξ≤5. Extrapolating the propagators to ξ→∞, we find the expected qualitative behavior. We provide arguments that our results are quantitatively reliable at least for values ξ≲1/2 of the gauge-fixing parameter. It is shown that the correlation functions, and, in particular, the ghost propagator, change significantly with increasing gauge parameter. In turn, the ghost-gluon running coupling as well as the position of the zero crossing of the Schwinger function of the gluon propagator remain within the uncertainties of our calculation unchanged.
M. Napetschnig, R. Alkofer, M. Q. Huber, J. M. Pawlowski, “Yang-mills propagators in linear covariant gauges from nielsen identities”, Phys. Rev. D 104, 054003 (2021).
https://journals.aps.org/prd/abstract/10.1103/PhysRevD.104.054003
Related to Project A02
Abstract:
We combine two non-perturbative approaches, one based on the two-particle-irreducible (2PI) action, the other on the functional renormalization group (fRG), in an effort to develop new non-perturbative approximations for the field theoretical description of strongly coupled systems. In particular, we exploit the exact 2PI relations between the two-point and four-point functions in order to truncate the infinite hierarchy of equations of the functional renormalization group. The truncation is ”exact” in two ways. First, the solution of the resulting flow equation is independent of the choice of the regulator. Second, this solution coincides with that of the 2PI equations for the two-point and the four-point functions, for any selection of two-skeleton diagrams characterizing a so-called Ф-derivable approximation. The transformation of the equations of the 2PI formalism into flow equations offers new ways to solve these equations in practice, and provides new insight on certain aspects of their renormalization. It also opens the possibility to develop approximation schemes going beyond the strict Ф-derivable ones, as well as new truncation schemes for the fRG hierarchy.
U. Reinosa, J.-P. Blaizot, J. M. Pawlowski, “Functional renormalization group and 2PI effective action formalism”, Annals Phys. 431, 168549 (2021).
https://www.sciencedirect.com/science/article/pii/S000349162100155X?via%3Dihub
Related to Project A02
Abstract:
We discuss the far-from-equilibrium evolution of ϕ3 theory in 1+1 dimensions with the temporal functional renormalization group. In particular, we show that this manifestly causal approach leads to novel one-loop exact equations for fully dressed correlation functions. Within this setup, we numerically compute the dynamical propagator. Its behavior suggests self-similarity far from equilibrium in a restricted momentum regime. We discuss the scaling exponents for our solution, as well as the numerical satisfaction of energy and particle number conservation. We also derive a simple exact representation of the expectation value of the energy-momentum tensor solely in terms of the propagator.
L. Corell, A. K. Cyrol, M. Heller, J. M. Pawlowski, “Flowing with the temporal renormalization group”, Phys. Rev. D 104, 025005 (2021).
https://journals.aps.org/prd/abstract/10.1103/PhysRevD.104.025005
Related to Project B03
Abstract:
Hadron production in relativistic nuclear collisions is well described in the framework of the Statistical Hadronization Model (SHM). We investigate the influence on SHM predictions of hadron mass spectra for light-flavor baryons and mesons modified by the addition of about 500 new states as predicted by lattice QCD and a relativistic quark model. The deterioration of the resulting thermodynamic fit quality obtained for Pb–Pb collision data at 2.76 TeV suggests that the additional states are not suited to be naively used since also interactions among the states as well as non-resonant contributions need to be considered in the SHM approach. Incorporating these effects via the pion nucleon interaction determined from measured phase shifts leads again to excellent reproduction of the experimental data. This is a strong indication that at least the additional nucleon excited states cannot be understood and used as independent resonances.
A. Andronic, P. Braun-Munzinger, D. Gündüz, Y. Kirchhoff, M. K. Köhler, J. Stachel, M. Winn, “Influence of modified light-flavor hadron spectra on particle yields in the statistical hadronization model”, Nuclear Physics A 1010, (2023).
https://www.sciencedirect.com/science/article/pii/S0375947421000415
Related to Project C05, A01, A02, C06
Abstract:
Real Clifford algebras for arbitrary numbers of space and time dimensions as well as their representations in terms of spinors are reviewed and discussed. The Clifford algebras are classified in terms of isomorphic matrix algebras of real, complex or quaternionic type. Spinors are defined as elements of minimal or quasi-minimal left ideals within the Clifford algebra and as representations of the pin and spin groups. Two types of Dirac adjoint spinors are introduced carefully. The relationship between mathematical structures and applications to describe relativistic fermions is emphasized throughout.
S. Floerchinger, “Real Clifford Algebras and Their Spinors for Relativistic Fermions ”, Universe 7, 168 (2021).
https://www.mdpi.com/2218-1997/7/6/168
Related to Project B03, C06
Abstract:
We present a comprehensive study of the quark sector of 2+1 flavor QCD, based on a self-consistent treatment of the coupled system of Schwinger-Dyson equations for the quark propagator and the full quark-gluon vertex in the one-loop dressed approximation. The individual form factors of the quark-gluon vertex are expressed in a special tensor basis obtained from a set of gauge-invariant operators. The sole external ingredient used as input to our equations is the Landau gauge gluon propagator with 2+1 dynamical quark flavors, obtained from studies with Schwinger-Dyson equations, the functional renormalization group approach, and large volume lattice simulations. The appropriate renormalization procedure required in order to self-consistently accommodate external inputs stemming from other functional approaches or the lattice is discussed in detail, and the value of the gauge coupling is accurately determined at two vastly separated renormalization group scales. Our analysis establishes a clear hierarchy among the vertex form factors. We identify only three dominant ones, in agreement with previous results. The components of the quark propagator obtained from our approach are in excellent agreement with the results from Schwinger-Dyson equations, the functional renormalization group, and lattice QCD simulation, a simple benchmark observable being the chiral condensate in the chiral limit, which is computed as (245 MeV)3. The present approach has a wide range of applications, including the self-consistent computation of bound-state properties and finite temperature and density physics, which are briefly discussed.
F. Gao, J. Papavassiliou, J. M. Pawlowski, “Fully coupled functional equations for the quark sector of QCD”, Phys. Rev. D 103, 094013 (2021).
https://journals.aps.org/prd/abstract/10.1103/PhysRevD.103.094013
Related to Project A02
Abstract:
We propose a novel simulation strategy for Yang-Mills theories with a complex coupling, based on the Lefschetz thimble decomposition. We envisage that the approach developed in the present work can also be adapted to QCD at finite density and real-time simulations. Simulations with Lefschetz thimbles offer a potential solution to sign problems in Monte Carlo calculations within many different models with complex actions. We discuss the structure of generalized Lefschetz thimbles for pure Yang-Mills theories with a complex gauge coupling β and show how to incorporate the gauge orbits. We propose to simulate such theories on the union of the tangential manifolds to the relevant Lefschetz thimbles attached to the critical manifolds of the Yang-Mills action. We demonstrate our algorithm on a (1+1)-dimensional U(1) model and discuss how, starting from the main thimble result, successive subleading thimbles can be taken into account via a reweighting approach. While we face a residual sign problem, our novel approach performs exponentially better than the standard reweighting approach.
J. M. Pawlowski, M. Scherzer, C. Schmidt, F. P. G. Ziegler, F. Ziesché, “Simulating Yang-Mills theories with a complex coupling”, Phys. Rev. D 103, 094505 (2021).
https://journals.aps.org/prd/abstract/10.1103/PhysRevD.103.094505
Related to Project A02
Abstract:
We investigate the dimensional crossover from three to two dimensions in an ultracold Fermi gas across the whole BCS-BEC crossover. Of particular interest is the strongly interacting regime as strong correlations and pair fluctuations are more pronounced in reduced dimensions. Our results are obtained from first principles within the framework of the functional renormalization group (FRG). Here, the confinement of the transverse direction is imposed by means of periodic boundary conditions. We calculate the equation of state, the gap parameter at zero temperature, and the superfluid transition temperature across a wide range of transversal confinement length scales. Particular emphasis is put on the determination of the finite-temperature phase diagram for different confinement length scales. In the end, our results are compared with recent experimental observations and we discuss them in the context of other theoretical works.
B. M. Faigle-Cedzich, J. M. Pawlowski, C. Wetterich, “Dimensional crossover in ultracold Fermi gases from functional renormalization”, Phys. Rev. A 103, 033320 (2021).
https://journals.aps.org/pra/abstract/10.1103/PhysRevA.103.033320
Related to Project C01
Abstract:
Reliably computing the free energy in a gauge theory like QCD is a challenging and resource-demanding endeavor. We explore the possibility to obtain the associated thermodynamic anomaly from two-point functions based on a conjectured relation. This conjecture is triggered by the relation to the Tan contact in condensed matter systems. For this investigation we use state-of-the-art results for the Yang-Mills gluon two-point function from the lattice and the functional renormalization group, as well as novel Dyson-Schwinger results at finite temperature computed in the present work. This allows for a first, qualitative, test of this conjecture. The results from all methods reveal the same nontrivial temperature behavior of the subleading large momentum dependence of the gluon propagator relevant for the conjectured relation. The comparison with the expected behavior for SU(2) Yang-Mills theory is encouraging to further pursue this approach.
O. Hajizadeh, M. Q. Huber, A. Maas, J. M. Pawlowski, “Exploring the Tan contact term in Yang-Mills theory”, Phys. Rev. D 103, 034023 (2021).
https://journals.aps.org/prd/abstract/10.1103/PhysRevD.103.034023
Related to Project A02, B03, C01, C05, C06
Abstract:
In this contribution, we discuss the asymptotic safety scenario for quantum gravity with a functional renormalization group approach that disentangles dynamical metric fluctuations from the background metric. We review the state of the art in pure gravity and general gravity–matter systems. This includes the discussion of results on the existence and properties of the asymptotically safe ultraviolet fixed point, full ultraviolet-infrared trajectories with classical gravity in the infrared, and the curvature dependence of couplings also in gravity–matter systems. The results in gravity–matter systems concern the ultraviolet stability of the fixed point and the dominance of gravity fluctuations in minimally coupled gravity–matter systems. Furthermore, we discuss important physics properties such as locality of the theory, diffeomorphism invariance, background independence, unitarity, and access to observables, as well as open challenges.
J. M. Pawlowski, M. Reichert, “Quantum Gravity: A Fluctuating Point of View”, Front. in
Phys. 8, 551848 (2021).
https://www.frontiersin.org/articles/10.3389/fphy.2020.551848/full
Related to Project A02
Abstract:
The description of hadron production in relativistic heavy-ion collisions in the statistical hadronization model is very good, over a broad range of collision energy. We outline this both for the light (u, d, s) and heavy (charm) quarks and discuss the connection it brings to the phase diagram of QCD.
A. Andronic, P. Braun-Munzinger, K. Redlich, J. Stachel, “Hadron yields in central nucleusnucleus
collisions, the statistical hadronization model and the QCD phase diagram”, Jan. 14, 2021, arXiv:2101.05747 (2021).
https://arxiv.org/abs/2101.05747
Related to Project C05
Abstract:
As a result of a nontrivial mixing matrix, neutrinos cannot be simultaneously in a flavor and mass eigenstate. We formulate and discuss information entropic relations that quantify the associated quantum uncertainty. We also formulate a protocol to determine the Pontecorvo-Maki-Nakagawa-Sakata (PMNS) matrix from quantum manipulations and measurements on an entangled lepton-neutrino pair. The entangled state features neutrino oscillations in a conditional probability involving measurements on the lepton and the neutrino. They can be switched off by choosing a specific observable on the lepton side which is determined by the PMNS matrix. The parameters of the latter, including the CP-violating phase δ, can be obtained by guessing them and improving the guess by minimizing the remaining oscillations.
S. Floerchinger, J.-M. Schwind, “Neutrino flavor-mass uncertainty relations and an entanglementassisted determination of the PMNS matrix”, Phys. Rev. D 102, 093001 (2020).
https://journals.aps.org/prd/abstract/10.1103/PhysRevD.102.093001
Related to Project C06, A06*
Abstract:
We present programmable two-dimensional arrays of microscopic atomic ensembles consisting of more than 400 sites with nearly uniform filling and small atom number fluctuations. Our approach involves direct projection of light patterns from a digital micromirror device with high spatial resolution onto an optical pancake trap acting as a reservoir. This makes it possible to load large arrays of tweezers in a single step with high occupation numbers and low power requirements per tweezer. Each atomic ensemble is confined to ~1 μm3 with a controllable occupation from 20 to 200 atoms and with (sub)-Poissonian atom number fluctuations. Thus, they are ideally suited for quantum simulation and for realizing large arrays of collectively encoded Rydberg-atom qubits for quantum information processing.
Y. Wang, S. Shevate, T. M. Wintermantel, M. Morgado, G. Lochead, S. Whitlock, “Preparation of hundreds of microscopic atomic ensembles in optical tweezer arrays”, npj Quantum Information 6 (2020).
https://www.nature.com/articles/s41534-020-0285-1
Related to Project A05
Abstract:
We exploit the concept of hydrodynamic attractors to establish a macroscopic description of the early time out-of-equilibrium dynamics of high energy heavy-ion collisions. One direct consequence is a general relation between the initial state energy and the produced particle multiplicities measured in experiments. When combined with an ab initio model of energy deposition, the entropy production during the preequilibrium phase naturally explains the universal centrality dependence of the measured charged particle yields in nucleus-nucleus collisions. Further, we estimate the energy density of the far-from-equilibrium initial state and discuss how our results can be used to constrain nonequilibrium properties of the quark-gluon plasma.
G. Giacalone, A. Mazeliauskas, S. Schlichting, „Hydrodynamic attractors, initial state energy
and particle production in relativistic nuclear collisions“, Phys. Rev. Lett. 123, 262301 (2019).
https://journals.aps.org/prl/abstract/10.1103/PhysRevLett.123.262301
Related to Project C06, A01, ABC
Abstract:
We derive a simple relation between strangeness neutrality and baryon-strangeness correlations. In heavy-ion collisions, the former is a consequence of quark number conservation of the strong interactions while the latter are sensitive probes of the character of QCD matter. This relation allows us to directly extract baryon-strangeness correlations from the strangeness chemical potential at strangeness neutrality. The explicit calculations are performed within a low-energy theory of QCD with 2+1 dynamical quark flavors at finite temperature and density. Nonperturbative quark and hadron fluctuations are taken into account within the functional renormalization group. The results show the pronounced sensitivity of baryon-strangeness correlations on the QCD phase transition and the crucial role that strangeness neutrality plays for this observable.
W. Fu, J. M. Pawlowski, and F. Rennecke, “Strangeness neutrality and baryon-strangeness correlations”, Phys. Rev. D 100, 111501 (2019).
https://journals.aps.org/prd/abstract/10.1103/PhysRevD.100.111501
Related to Project A01, A02, B03, C05, C06
Abstract:
Measurements of anisotropic flow coefficients (𝑣𝑛) and their cross-correlations using two- and multiparticle cumulant methods are reported in collisions of 𝑝𝑝 at √𝑠=13 TeV, 𝑝−Pb at a center-of-mass energy per nucleon pair √𝑠NN=5.02 TeV, Xe-Xe at √𝑠NN=5.44 TeV, and Pb-Pb at √𝑠NN=5.02 TeV recorded with the ALICE detector. The multiplicity dependence of 𝑣𝑛 is studied in a very wide range from 20 to 3000 particles produced in the midrapidity region |𝜂|<0.8 for the transverse momentum range 0.2<𝑝𝑇<3.0 GeV/𝑐. An ordering of the coefficients 𝑣2>𝑣3>𝑣4 is found in 𝑝𝑝 and 𝑝−Pb collisions, similar to that seen in large collision systems, while a weak 𝑣2 multiplicity dependence is observed relative to nucleus-nucleus collisions in the same multiplicity range. Using a novel subevent method, 𝑣2 measured with four-particle cumulants is found to be compatible with that from six-particle cumulants in 𝑝𝑝 and 𝑝−Pb collisions. The magnitude of the correlation between 𝑣2𝑛 and 𝑣2𝑚, evaluated with the symmetric cumulants SC(𝑚,𝑛) is observed to be positive at all multiplicities for 𝑣2 and 𝑣4, while for 𝑣2 and 𝑣3 it is negative and changes sign for multiplicities below 100, which may indicate a different 𝑣𝑛 fluctuation pattern in this multiplicity range. The observed long-range multiparticle azimuthal correlations in high multiplicity 𝑝𝑝 and 𝑝−Pb collisions can neither be described by pythia 8 nor by impact-parameter-Glasma, music, and ultrarelativistic quantum molecular dynamics model calculations, and hence, provide new insights into the understanding of collective effects in small collision systems.
[ALICE Collaboration] A. Dubla, S. Masciocchi, I. Selyuzhenkov et al., „Investigations of Anisotropic
Flow Using Multiparticle Azimuthal Correlations in pp, p-Pb, Xe-Xe, and Pb-Pb Collisions at the LHC“, Phys. Rev. Lett. 123, 142301 (2019).
https://journals.aps.org/prl/abstract/10.1103/PhysRevLett.123.142301
Related to Project C06, ABC
Abstract:
We investigate the dynamics of axion-like particle (ALP) dark matter where the field range is enlarged by a monodromy. The monodromy potential allows sufficient production of dark matter also at larger couplings to the Standard Model particles. The potential typically features a number of “wiggles” that lead to a rapid growth of fluctuations. Using classical-statistical field theory simulations we go beyond the linear regime and treat the system in the non-linear and even non-perturbative regime. For sufficiently strong wiggles the initially homogeneous field is completely converted into fluctuations. The fluctuations correspond to dark matter particles with a non-vanishing velocity and we consider the corresponding restrictions from structure formation as well as the effects on today’s dark matter density. Since all the dark matter is made up from these strong fluctuations, the dark matter density features large,  (1) fluctuations at scales ≲ 106 km√eV/ma.
(1) fluctuations at scales ≲ 106 km√eV/ma.
J. Berges, A. Chatrchyan und J. Jaeckel, „Foamy dark matter from monodromies“, JCAP 1908,020 (2019).
https://iopscience.iop.org/article/10.1088/1475-7516/2019/08/020
Related to Project B02, B03
Abstract:
Quantum anomalies are violations of classical scaling symmetries caused by divergences that appear in the quantization of certain classical theories. Although they play a prominent role in the quantum field theoretical description of many-body systems, their influence on experimental observables is difficult to discern. In this study, we discovered a distinctive manifestation of a quantum anomaly in the momentum-space dynamics of a two-dimensional (2D) Fermi superfluid of ultracold atoms. The measured pair momentum distributions of the superfluid during a breathing mode cycle exhibit a scaling violation in the strongly interacting regime. We found that the power-law exponents that characterize long-range phase correlations in the system are modified by the quantum anomaly, emphasizing the influence of this effect on the critical properties of 2D superfluids.
P. A. Murthy, N. Defenu, L. Bayha, M. Holten, P. M. Preiss, T. Enss und S. Jochim, „Quantum
scale anomaly and spatial coherence in a 2D Fermi superfluid“, Science 365, 268 (2019).
https://www.science.org/doi/10.1126/science.aau4402
Related to Project C01, C02, ABC
Abstract:
Nonthermal fixed points in the evolution of a quantum many-body system quenched far out of equilibrium manifest themselves in a scaling evolution of correlations in space and time. We develop a low-energy effective theory of nonthermal fixed points in a bosonic quantum many-body system by integrating out long-wavelength density fluctuations. The system consists of 𝑁 distinguishable spatially uniform Bose gases with U(𝑁)-symmetric interactions. The effective theory describes interacting Goldstone modes of the total and relative-phase excitations. It is similar in character to the nonlinear Luttinger-liquid description of low-energy phonons in a single dilute Bose gas, with the markable difference of a universal nonlocal coupling function depending, in the large-𝑁 limit, only on momentum, single-particle mass, and density of the gas. Our theory provides a perturbative description of the nonthermal fixed point, technically easy to apply to experimentally relevant cases with a small number of fields 𝑁. Numerical results for 𝑁=3 allow us to characterize the analytical form of the scaling function and confirm the analytically predicted scaling exponents. The predicted and observed exponentially suppressed coherence at short distances takes the form of that of a quasicondensate in low-dimensional equilibrium systems. The fixed point which is dominated by the relative phases is found to be Gaussian, while a non-Gaussian fixed point is anticipated to require scaling evolution with a distinctly lower power of time.
A. N. Mikheev, C.-M. Schmied und T. Gasenzer, „Low-energy effective theory of nonthermal
fixed points in a multicomponent Bose gas“, Phys. Rev. A 99, 063622 (2019).
https://journals.aps.org/pra/abstract/10.1103/PhysRevA.99.063622
Related to Project A04, B03
Abstract:
A fundamental challenge in digital quantum simulation (DQS) is the control of an inherent error, which appears when discretizing the time evolution of a quantum many-body system as a sequence of quantum gates, called Trotterization. Here, we show that quantum localization-by constraining the time evolution through quantum interference-strongly bounds these errors for local observables, leading to an error independent of system size and simulation time. DQS is thus intrinsically much more robust than suggested by known error bounds on the global many-body wave function. This robustness is characterized by a sharp threshold as a function of the Trotter step size, which separates a localized region with controllable Trotter errors from a quantum chaotic regime. Our findings show that DQS with comparatively large Trotter steps can retain controlled errors for local observables. It is thus possible to reduce the number of gate operations required to represent the desired time evolution faithfully.
M. Heyl, P. Hauke, P. Zoller, “Quantum localization bounds Trotter errors in digital quantum simulation”, Science Advances 5 (2019).
https://www.science.org/doi/10.1126/sciadv.aau8342
Related to Project B04
Abstract:
Hydrokinetic theory of thermal fluctuations is applied to a nonconformal relativistic fluid. Solving the hydrokinetic equations for an isotropically expanding background we find that hydrodynamic fluctuations give ultraviolet divergent contributions to the energy-momentum tensor. After shifting the temperature to account for the energy of nonequilibrium modes, the remaining divergences are renormalized into local parameters, e.g., pressure and bulk viscosity. We also confirm that the renormalization of the pressure and bulk viscosity is universal by computing them for a Bjorken expansion. The fluctuation-induced bulk viscosity reflects the nonconformal nature of the equation of state and is modestly enhanced near the QCD deconfinement temperature.
Y. Akamatsu, A. Mazeliauskas und D. Teaney, „Bulk viscosity from hydrodynamic fluctuations
with relativistic hydrokinetic theory“, Phys. Rev. C 97, 024902 (2018).
https://journals.aps.org/prc/abstract/10.1103/PhysRevC.97.024902
Related to Project C06. A01
Abstract:
We study the impact of attractive self-interactions on the nonequilibrium dynamics of relativistic quantum fields with large occupancies at low momenta. Our primary focus is on Bose-Einstein condensation and nonthermal fixed points in such systems. For a model system, we consider O(N)-symmetric scalar field theories. We use classical-statistical real-time simulations as well as a systematic 1/N expansion of the quantum (two-particle-irreducible) effective action to next-to-leading order. When the mean self-interactions are repulsive, condensation occurs as a consequence of a universal inverse particle cascade to the zero-momentum mode with self-similar scaling behavior. For attractive mean self-interactions, the inverse cascade is absent, and the particle annihilation rate is enhanced compared to the repulsive case, which counteracts the formation of coherent field configurations. For N≥2, the presence of a nonvanishing conserved charge can suppress number-changing processes and lead to the formation of stable localized charge clumps, i.e., Q balls.
J. Berges, K. Boguslavski, A. Chatrchyan und J. Jaeckel, „Attractive vs. repulsive interactions
in the Bose-Einstein condensation dynamics of relativistic field theories“, Phys. Rev. D 96,2017 (2017).
https://journals.aps.org/prd/abstract/10.1103/PhysRevD.96.076020
Related to Project A03, A04, A05, B03